An Incompletely specified function is a Boolean function that only define output values for a subset of its inputs - i.e. a Boolean function whos output is a don't care for at least one of its input combinations. Incompletely specified functions often make no guarantees as to the unspecified output whatsoever.
Overview[edit]
| A | B | C | |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | X |
| 0 | 1 | 0 | X |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | X |
In many situations when working with combinational circuits, some combinations of inputs should not occur under normal working conditions. For circuits with such combinations, those combinations can be treated as either 0 or 1 depending on whichever yields a more simplified Boolean expression.
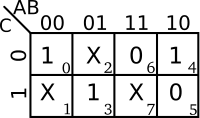
Boolean functions with don't care output terms are represented with a . For example consider the following function.
Which can be represented with the following truth table and K-map.
Note that depending on the final design of the circuit, the output for for example may be either 0 or 1.
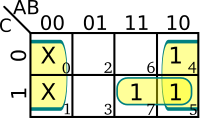
K-map[edit]
- Main article: karnaugh_map#Don't cares
Karnaugh maps are especially suitable for minimizing logic circuts with don't care outputs because they directly translate to don't care cells on a k-map. If grouping don't care cells results in larger groups, then more variables may be eliminated resulting in smaller Boolean expressions.
Properties[edit]
| This section is empty; you can help add the missing info by editing this page. |