Boolean algebra (or less commonly symbolic logic) is a branch of algebra that deals with only two logic values - 0 (corresponding to false) and 1 (corresponding to true).

Today, Boolean algebra is the primary mathematical tool used in designing modern digital systems. Switching functions are described using Boolean algebra since they deal with two discrete states - ON and OFF (or 1 and 0). Those functions are in turn implemented via transistors which act as switches, a natural implementation for representing Boolean algebra operations. Once primitive Boolean operation circuits such as NOT, AND, and OR gates are implemented, any conceivable system of logic can be implemented using them like Lego pieces.

Variables

Main articles: Boolean Variables and boolean data type

Boolean algebra uses variables just like normal algebra. Those variables can only have one of two values - either a 0 or a 1. Variable are commonly represented as a single alphabet letter. While there is no one acceptable convention, a it's not uncommon to see letters such as used for inputs and for output. That's also the convention used on WikiChip. Sometimes it's desired to represent the negated (opposite) value of a variable, that's often done with a bar or a tick (prime) above or next to the letter, for example or although other notations exist. is read "not A", regardless of notation.

0 & 1

Boolean algebra deals with only two unique states or values. We often represent those two values as and . However it's important to understand that those are just two convenient representations. This is often written as . You can assign and instead and the math should work just fine.

Operations & Truth tables

Main articles: Boolean Operations and truth table

Boolean algebra has a set of operations that can be performed on Boolean values, those operations are conveniently enough called binary operations. The three common Boolean operators are AND, OR, and NOT. Understanding those operators can better be done by examining their behavior via tool called a truth table. truth tables is a table that lists all possible input values and their respective output values. Truth tables can be said to be the unique signature of a specific Boolean function. Truth tables are an excellent way of seeing the relationships between input values and given Boolean expressions. While there may be many ways to realize or construct a Boolean function to represent a specific relation, they all share the very same truth table. A truth-vector is a truth table in vector form.

AND operator

Main article: conjunction

Inputs		Outputs
A	B	Q
0	0	0
0	1	0
1	0	0
1	1	1

The Boolean operator AND is usually represented by either , , or no symbol at all: for example "", "", and "" are all equivalent and are read "A AND B". The behavior of this operator is shown in the truth table on the right. The result of "A AND B" is true if both A and B are true; otherwise the result is false. This expression is also called a Boolean product.

For example, suppose we have the function

Or

OR operator

Main article: disjunction

Inputs		Outputs
A	B	Q
0	0	0
0	1	1
1	0	1
1	1	1

The Boolean operator OR is usually represented by or operators. For example "" and "". The expression is read "A or B". The result of "A OR B" is true if either A is true or B is true; otherwise the result is false. This expression is also called a Boolean sum.

For example, suppose we have the function

Or

NOT operator

Main article: negation

Inputs	Outputs
A	Q
0	1
1	0

The Boolean operator NOT is represented by many notations, the three most popular ones are "", "", and "". Note that unlike the AND and OR operators, the NOT operator is a unary operator and is thus drawn above or on the side of the variable. The expression is read "not A". The truth table for the NOT operator is shown on the right. The result of the NOT operator is true if A is false, otherwise the result is true. This expression is called a Boolean complement.

For example, suppose we have the function

Or

Order of operations

Main article: Order of Operations

So far we've made it simple by explicitly using parenthesis in all of our examples to indicate a certain part of the expression is evaluated before another part. The order of operations of a Boolean expression is very important to obtain correct result. For example consider the function for input . Does it mean ? or does it mean ? Same expression, different results. It turns out the the correct order is (and ). In Boolean expressions, the NOT operator has the highest precedence, followed by AND, then OR.

For example,

and

Axioms

Main article: Boolean Algebra Axioms

Boolean algebra is govern by a set of special axioms that say what kind of Boolean expression manipulations can be done. They are called axioms because they not things that have to be proven but rather part of the definition of Boolean algebra. Many of those laws are common to both Boolean algebra and ordinary algebra. Using those laws, equations can be converted into different forms. One particular transformation known as minimization plays a crucial role in the design of logic circuits. One last thing to note before we get to the actual laws is that Boolean algebra identities come in pairs. This is known as duality principle and it is covered in much more detail later on.

Axiom	AND form	OR form
Identity Axiom
Inverse Axiom
Commutative Axiom
Associative Axiom
Distributive Axiom

In addition to those five axioms, there are a number of other handful laws. Those laws can be proven using the axioms we've introduced above.

Law	AND form	OR form
Complement Law
Dominance Law
Idempotent Law
Absorption Law
DeMorgan's Law
Involution Law

It's interesting to note that it's easy to see the divergence between Boolean algebra and ordinary algebra from those laws. For example consider . From Dominance Law we know the answer is . This is clearly not true for ordinary algebra where . Likewise from the Absorption Law we know that while in ordinary algebra this is not true either.

Axioms explanation

The Identity Axiom simply states that any expression ANDed with 1 or ORed with 0 results in the original expression. Identity elements or simply identities are elements that when used with their appropriate operator leave the original element unchanged. In the case of Boolean algebra, the identity element for AND is 1 and 0 for OR.

Example:

The Inverse Axiom simply states that when you AND or OR an expression with its complement results in the identity element for that operation.

Example:

The Commutative Axiom states that individual elements in an expressions can be reordered without affecting the meaning of the expression. For example .

The Associative Axiom states that individual elements in an expression can be regrouped without affecting the meaning of the expression. For example . Simply put, it makes no difference in what order you group the expressions when ANDing or ORing several expressions together.

The Distributive Axiom states that ANDing distributes over over ORing. That is, ORing several expressions and ANDing the result is equaivilent to ANDing the result with a each of the individual expressions then ORing the product. Often times the Distributive Axiom is applied in reverse in a similar way to factoring in ordinary algebra. For example, given , the expression can be factored out to

Canonical Forms

a	b	c	minterms	notation
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Earlier we've covered truth tables which are like signatures; there are many ways to represent the same logic, however it will always result in the very same truth table. When two Boolean functions result in the same exact truth table, the two functions are said to be logically equivalent. The different representations of a truth table are known as forms. In an attempt to eliminate confusion, a few forms were were chosen to be canonical or standard forms. Before we describe those forms we need to go over a few terms.

Sum of Products (SoP)

A minterm is the Boolean product (ANDing) of variables and contains all variables of the function just once, in either normal or complemented form. For example, for the function with two variables, we can have the following minterms: , , , and . If the value assigned to a variable is 0, the variable is complemented, conversely a variable remains uncomplemented if the value assigned to it is 1. Consider the table to the right, since in the first row, the variables , , and are all , the minterms for them is

A sum term is the Boolean sum (ORing) of variables as a subset of the possible variables or their complements. For example, for the function , the following are a few possible sum terms: , , and .

The sum of minterms also called Sum of Product (SoP), canonical sum of products, minterm expansion, and canonical disjunctive normal form (CDNF) is a Boolean expression in which each term contains all the variables, either in normal or complemented form as sum of all the minterms. For example, consider the following Boolean functions.

We can express that function in SoP form as follows.

Sum of Product Example
Function
a	b	c	minterms	notation
0	0	0			0	1
0	0	1			0	1
0	1	0			0	1
0	1	1			1	0
1	0	0			1	0
1	0	1			1	0
1	1	0			1	0
1	1	1			1	0

The minterms for which the function produces a are called 1-minterms. Likewise, minterms for which the function produces a are called 0-minterms. Any Boolean function can be expressed as sum of its 1-minterms. For example, consider the following function:

The truth table for it is on the right. We can express this function as sum of 1-minterms:

We can replace the individual minterms with their respective index which is also shown in the table.

This function can now be more concisely written a in the following way:

I.e.

Likewise, the inverse of the function can be expressed as the sum of 0-minterms:

Product of Sum (PoS)

Sum of Product Example
Function
a	b	c	minterms	notation
0	0	0			0	1
0	0	1			0	1
0	1	0			0	1
0	1	1			1	0
1	0	0			1	0
1	0	1			1	0
1	1	0			1	0
1	1	1			1	0

A maxterm is the Boolean sum (ORing) of variables and contains all variables of the function just once, in either normal or complemented form. For example, for the function with two variables, we can have the following maxterms: , , , and .

A product term is the Boolean product (ANDing) of variables as a subset of the possible variables or their complements. For example, for function , the following are possible product terms: , , and .

The sum of maxterms also called Product of Sum (PoS), canonical sum of products, maxterm expansion, canonical conjunctive normal form (CCNF) is a Boolean expression in which each term contains all the variables, either in normal or complemented form as the sum of all the maxterms.

We can express that function in PoS form as follows.

The maxterms for which the function produces a are called 1-maxterms. Likewise, maxterms for which the function produces a are called 0-maxterms. Any Boolean function can be expressed as product of its 0-maxterms. For example, consider the following function:

The truth table for it is on the right. We can express this function as product of 0-maxterms:

We can replace the individual minterms with their respective index which is also shown in the table.

This function can now be more concisely written a in the following way:

I.e.

Likewise, the inverse of the function can be expressed as the product of 0-maxterms:

Minimization

Main article: logic minimization

Generating Boolean functions for certain logic is often pretty straightforward. On many occasions, however, those functions might be more complicated than they have to be. Minimization is the process of transforming a Boolean function into its smallest equivalent form. While the best circuit design depends on the technology involved, minimization usually translates directly into smaller circuits and lower implementation costs (areas, time, et al).

One way to minimize a Boolean expression is to simply massage the expression using the axioms and laws described earlier on. Such process is heuristic in nature and thus there is no one algorithm or rules that must be followed. For example, consider the following function . It can be hand minimized as:

Karnaugh Map

Main article: Karnaugh Map

While minimization function through manual massaging of expressions works for basic functions, it becomes incredibly complex and time consuming as you increase the number of terms and variables involved. A Karnaugh Map (or K-Map) is technique that provides a systematic way to simplify as well as manipulate Boolean expressions.

Truth Table
Inputs			Outputs
A	B	C	Q
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

A K-Map is a actually a truth table that has been rearranged in a number of important ways to make it possible to visually find the expression we're looking for. An -variable K-Map is table consisting of cells, each representing a single minterm. For each minterm where the function results in a , we put a 1. Conversely, for each minterm where the function results in a , we put a zero - or more commonly, we leave blank.

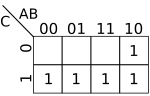
Let's consider the following 3-variable Boolean function: . Because this function has 3 variables, we need a 3-variable K-Map which means we're working with an 8-cell table. Note the special arrangement of the columns and rows. Particularly, between two adjacent row and columns, only a single variable is allowed to transition from 0 to 1 or 1 to 0. As a result, after "01" we move to "11" instead of "10" which would result in both variables transitioning between 0 and 1. For 3 variables, the table is arranged in 4 columns of 2 rows each. 2 of the variables span the columns while the last variable spans the rows. Our choice for which variable goes where was arbitrary. Any way you want will work so long the k-map is constructed correctly based on a truth table.

For every minterm in the truth table where the output is we mark 1 on the K-Map. The cells that result in are left blank for convenience. Once the k-map represents the entire truth table, visually inspect the table and locate the largest groups of adjacent squares containing 1. Those groups must have power of 2 number of cells; i.e. a group can only be of size 1, 2, 4, 8, etc.. A group of 3 cells thus must be broken down into 2 groups of 2 where one cell overlaps (see the k-map article for a more detailed explanation). In our K-Map, we have 1 group of 4 cells and another group of just 2 cells.

For each group marked down we look which variables are common to all the cells in the group. For the group consisting of four cells neither a nor b are common since they both change, however c is always 1 for all four cells. Therefore the expression for that group is simply . For the second group with just two cells, c is no loner common to the group. However both a and b are now common since neither of them change. Because a is always 1 and b is always 0 in that group, the expression for the second group is . The final simplified expression is the SoP: . I.e.:

Quine-McCluskey Method

Main article: Quine-McCluskey Method

The Quine-McCluskey Method (QMM) is an algorithm developed for minimizing Boolean expressions. This algorithm is functionally identical to how a K-Map works but orients itself in tabular form. Due to its algorithmic nature, it's much more suitable to be implemented as a program and can be easily applied to any number of variables and terms. QMM is used in various EDA tools.

Boolean functions

Main article: Boolean Function

A Boolean function is an algebraic function of the form where is defined as Boolean domain and . There are possible Boolean functions for Boolean variables.

Properties of functions

Main article: Boolean Function Properties

The properties of Boolean functions have been a subject of extensive research especially in conjunction with the switching theory. Understanding the properties of the Boolean functions has proven to help in various stages of logic design (e.g. logic synthesis). Below are some of the more important properties of Boolean functions.

Duality Principle

Main article: Duality Principle

Earlier on it was pointed out that every axiom and every law has an OR form and an AND form. The Duality Principle simply state that when you take a valid Boolean statement and interchange all with and with and vice vesa, you obtain its dual which is also a valid Boolean statement.

Consider the following statement which happens to be DeMorgan's Law. Then by the duality principle we also know that must also be true. Indeed that is the second form of the law.

Self-dual function

Main article: Self-dual Boolean function

A Boolean function is said to be a self-dual function if it is equivalent to the same function with all inputs and outputs inverted. For example consider the majority function. It is defined as:

We can derive it's dual function by inverting the inputs and outputs:

Since , the majority function is said to be a self-dual function.

Monotonic functions

Main article: Monotonic Functions

The monotonicity property of Boolean functions says that for two Boolean vectors a and b such that ; if then is a monotonically increasing function. Conversely, if then is a monotonically decreasing function. In other words, a monotonically increasing (or decreasing) function never has its output changes from one to a zero (or zero to a one for decreasing) by changing zero to a one in the input. Monotonic functions can be constructed with just ANDs and ORs operations without negation. By an extension, monotone circuits are circuits in which only AND and OR gates.

Unate functions

Main article: Unate Boolean Function

This section is empty; you can help add the missing info by editing this page.

Linear functions

Main article: Linear Boolean Functions

A linear function is either the constant function or the exclusive OR of variables. That is, is one that has the form

For example, consider the following function . Since we can write it in the polynomial form above (i.e. ), it's a linear function.

0/1 Preserving functions

Main articles: 0-Preserving Boolean Function and 1-Preserving Boolean Function

A Boolean function is said to be 0-preserving if . Likewise a Boolean function is said to be 1-preserving if .

functional completeness

Main article: Functional Completeness

A set of Boolean functions is said to be universal or complete iif it's 0-preserving, 1-preserving, Self-dual, monotonically increasing, and linear. A complete set can form any other Boolean expression by combining the functions in the set.

Complementary Function

This section is empty; you can help add the missing info by editing this page.

Additional Logical connectives

Main article: Logical connective

In additional to the basic AND, OR, and NOT, there are a number of other logical connectives.

XOR

Main article: xor

This section is empty; you can help add the missing info by editing this page.

conditional

Main article: conditional

Inputs		Outputs
A	B	Q
0	0	1
0	1	1
1	0	0
1	1	1

It's often necessary to express things in the form . In that form, is called a conditional, is the antecedent, and is the consequent. In order for the expression to hold, when is true, must also be true. However, conversely, when is false, the statement is trivially true regardless of .

biconditional

Main article: biconditional

Inputs		Outputs
A	B	Q
0	0	1
0	1	0
1	0	0
1	1	1

A proposition in the form is called biconditional and represents the truth function: A if and only if B. The truth table is thus identical to . In fact, the standard method of proving biconditional is to prove and then to prove .

Propositional calculus

Main article: propositional calculus

This section is empty; you can help add the missing info by editing this page.

Posets and Lattices

This section is empty; you can help add the missing info by editing this page.

Diagrammatic representations

This section is empty; you can help add the missing info by editing this page.

Venn Diagram

This section is empty; you can help add the missing info by editing this page.

Logic Diagram

This section is empty; you can help add the missing info by editing this page.

Hasse Diagram

This section is empty; you can help add the missing info by editing this page.

Additional topics

This section is empty; you can help add the missing info by editing this page.

See also

• Karnaugh Map