MAJ Gate
Typical Symbol
Functional
Truth Table
3-input Majority Gate
Inputs
Outputs
A
B
C
Q
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
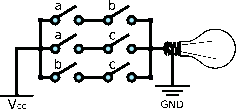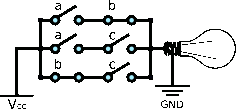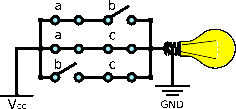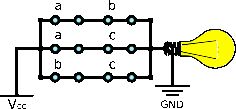
The majority gate (MAJ gate ) is a logic gate that implements the majority function - a device that outputs a HIGH when the majority of its inputs are HIGH, otherwise it outputs a LOW .
Applications MAJ3 Maj gate on CMOS (AOI222)
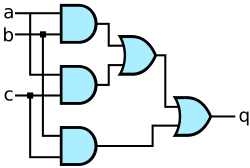
A 3-input MAJ gate (MAJ3) can be implemented as
Equation
left-parenthesis a logical-and b right-parenthesis logical-or left-parenthesis a logical-and c right-parenthesis logical-or left-parenthesis b logical-and c right-parenthesis
.
CMOS However the naive implementation will result in up to 30 transistors. Since
Equation
MAJ left-parenthesis a comma b comma c right-parenthesis equals ModifyingAbove Above ModifyingAbove MAJ left-parenthesis a comma b comma c right-parenthesis With bar With bar
,we can define MAJ3 as
Equation
MAJ left-parenthesis a comma b comma c right-parenthesis equals ModifyingAbove Above ModifyingAbove left-parenthesis a logical-and b right-parenthesis logical-or left-parenthesis a logical-and c right-parenthesis logical-or left-parenthesis b logical-and c right-parenthesis With bar With bar
and that can be implemented using a single AOI222 which is defined as
Equation
AOI 222 left-parenthesis a comma b comma c comma d comma e comma f right-parenthesis equals ModifyingAbove left-parenthesis a logical-and b right-parenthesis logical-or left-parenthesis c logical-and d right-parenthesis logical-or left-parenthesis e logical-and f right-parenthesis With bar
note that by substituting a, b, and c for d, e, and f we get MAJ:
Equation
MAJ left-parenthesis a comma b comma c right-parenthesis equals ModifyingAbove upper A upper O upper I Baseline 222 left-parenthesis a comma b comma c comma a comma b comma c right-parenthesis With bar
It can also be implemented using a OAI222 gate the very same way. Since
Equation
OAI 222 left-parenthesis a comma b comma c comma d comma e comma f right-parenthesis equals ModifyingAbove left-parenthesis a logical-or b right-parenthesis logical-and left-parenthesis c logical-or d right-parenthesis logical-and left-parenthesis e logical-or f right-parenthesis With bar
,then
Equation
MAJ left-parenthesis a comma b comma c right-parenthesis equals ModifyingAbove upper O upper A upper I Baseline 222 left-parenthesis a comma b comma c comma a comma b comma c right-parenthesis With bar
MAJ5 A MAJ5 can be naively described as the OR of 10 MAJ3 gates. It can be simplified down to 10 AND gates and 9 OR gates by rewriting the terms:[1 ]
Equation
MAJ 5 left-parenthesis upper A comma upper B comma upper C comma upper D comma upper E right-parenthesis equals left-parenthesis upper A logical-and left-parenthesis left-parenthesis upper B logical-and left-parenthesis upper C logical-or upper D logical-or upper E right-parenthesis right-parenthesis logical-or left-parenthesis upper C logical-and left-parenthesis upper D logical-or upper E right-parenthesis right-parenthesis logical-or left-parenthesis upper D logical-and upper E right-parenthesis right-parenthesis right-parenthesis logical-or left-parenthesis upper B logical-and left-parenthesis upper C logical-and left-parenthesis upper D logical-or upper E right-parenthesis right-parenthesis logical-or left-parenthesis upper D logical-and upper E right-parenthesis right-parenthesis logical-or left-parenthesis upper C logical-and upper D logical-and upper E right-parenthesis
This is probably optimal, since the optimal sorting network of 5 terms has 9 comparisons.
See also ↑ Ralph L. DeCarli (2009). The Majority Gate