Semiconductor & Computer Engineering
From WikiChip
Difference between revisions of "majority gate"
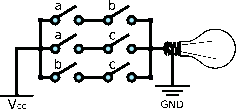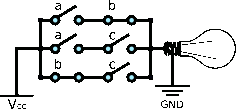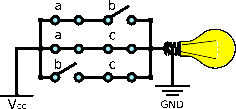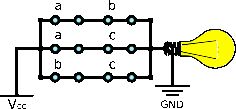
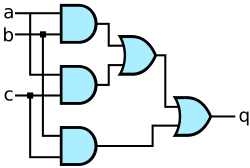
(MAJ5) |
|||
| Line 12: | Line 12: | ||
== MAJ3 == | == MAJ3 == | ||
| − | + | [[File:MAJ3 gate.svg|frameless|right|250px]] | |
| + | [[File:maj gate (cmos).svg|thumb|right|200px|Maj gate on CMOS (AOI222)]] | ||
A 3-input MAJ gate (MAJ3) can be implemented as <math>(a \land b) \lor (a \land c) \lor (b \land c)</math>. | A 3-input MAJ gate (MAJ3) can be implemented as <math>(a \land b) \lor (a \land c) \lor (b \land c)</math>. | ||
===CMOS=== | ===CMOS=== | ||
| Line 19: | Line 20: | ||
we can define MAJ3 as | we can define MAJ3 as | ||
:<math>\text{MAJ}(a, b, c) = \overline{\overline{(a \land b) \lor (a \land c) \lor (b \land c)}}</math> | :<math>\text{MAJ}(a, b, c) = \overline{\overline{(a \land b) \lor (a \land c) \lor (b \land c)}}</math> | ||
| − | and that can be implemented using a single [[ | + | and that can be implemented using a single [[Wikipedia:AND-OR-Invert|AOI222]] which is defined as |
:<math>\text{AOI222}(a, b, c, d, e, f) = \overline{(a \land b) \lor (c \land d) \lor (e \land f)}</math> | :<math>\text{AOI222}(a, b, c, d, e, f) = \overline{(a \land b) \lor (c \land d) \lor (e \land f)}</math> | ||
note that by substituting ''a, b, and c'' for ''d, e, and f'' we get MAJ: | note that by substituting ''a, b, and c'' for ''d, e, and f'' we get MAJ: | ||
| Line 27: | Line 28: | ||
then | then | ||
:<math>\text{MAJ}(a, b, c) = \overline{OAI222(a, b, c, a, b, c)}</math> | :<math>\text{MAJ}(a, b, c) = \overline{OAI222(a, b, c, a, b, c)}</math> | ||
| − | |||
| − | |||
== MAJ5 == | == MAJ5 == | ||
| − | A MAJ5 can be naively described as the OR of 10 MAJ3 gates. It can be simplified down to 10 AND gates and 9 OR gates by rewriting the terms | + | A MAJ5 can be naively described as the OR of 10 MAJ3 gates. It can be simplified down to 10 AND gates and 9 OR gates by rewriting the terms:<ref>Ralph L. DeCarli (2009). [https://www.sysmatrix.net/~omnivore/MajorityGate.html The Majority Gate]</ref> |
| + | :<math>\text{MAJ5}(a, b, c) = ( A \land ( ( B \land (C \lor D \lor E) ) \lor ( C \land (D \lor E) ) \lor (D \land E) ) ) \lor ( B \land ( C \land (D \lor E) ) \lor (D \land E) ) \lor ( C \land D \land E )</math> | ||
| + | |||
| + | This is probably optimal, since the optimal sorting network of 5 terms has 9 comparisons. | ||
== See also == | == See also == | ||
* [[logic gates]] | * [[logic gates]] | ||
* [[compound logic gates]] | * [[compound logic gates]] | ||
Revision as of 23:29, 7 May 2020
| MAJ Gate | ||||||||||||||||||||||||||||||||||||||||||||
| Typical Symbol | ||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||
| Functional | ||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||
| Truth Table | ||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||
The majority gate (MAJ gate) is a logic gate that implements the majority function - a device that outputs a HIGH when the majority of its inputs are HIGH, otherwise it outputs a LOW.
Contents
Applications
 |
This section is empty; you can help add the missing info by editing this page. |
MAJ3
.svg)
A 3-input MAJ gate (MAJ3) can be implemented as .
CMOS
However the naive implementation will result in up to 30 transistors. Since
- ,
we can define MAJ3 as
and that can be implemented using a single AOI222 which is defined as
note that by substituting a, b, and c for d, e, and f we get MAJ:
It can also be implemented using a OAI222 gate the very same way. Since
- ,
then
MAJ5
A MAJ5 can be naively described as the OR of 10 MAJ3 gates. It can be simplified down to 10 AND gates and 9 OR gates by rewriting the terms:[1]
This is probably optimal, since the optimal sorting network of 5 terms has 9 comparisons.