| Line 3: | Line 3: | ||
==Overview== | ==Overview== | ||
| + | {| class="wikitable" style="float: right; width: 140px; text-align: center;" | ||
| + | ! A !! B !! C !! <math>f</math> | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 1 | ||
| + | |- | ||
| + | | 0 || 0 || 1 || {{X}} | ||
| + | |- | ||
| + | | 0 || 1 || 0 || {{X}} | ||
| + | |- | ||
| + | | 0 || 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || 0 || 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 || 1 || 0 | ||
| + | |- | ||
| + | | 1 || 1 || 0 || 0 | ||
| + | |- | ||
| + | | 1 || 1 || 1 || {{X}} | ||
| + | |} | ||
In many situations when working with [[combinational circuit]]s, some combinations of inputs [[can't happen|should not occur]] under normal working conditions. For circuits with such combinations, those combinations can be treated as either 0 or 1 depending on whichever yields a more [[logic minimization|simplified]] Boolean expression. | In many situations when working with [[combinational circuit]]s, some combinations of inputs [[can't happen|should not occur]] under normal working conditions. For circuits with such combinations, those combinations can be treated as either 0 or 1 depending on whichever yields a more [[logic minimization|simplified]] Boolean expression. | ||
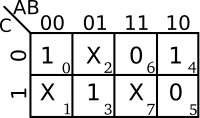
| + | Boolean functions with don't care output terms are represented with a <math>d</math>. For example consider the following function. | ||
| + | ::<math>f(A,B,C) = \sum m(0,3,4)+d(1,2,7)</math> | ||
| + | Which can be represented with the following [[truth table]] and [[K-map]]. | ||
| − | + | ::[[File:kmap unspecified func example.svg|200px]] | |
| + | |||
| + | Note that depending on the final design of the circuit, the output for <math>f(0,0,1)</math> for example may be either 0 or 1. | ||
Revision as of 18:12, 15 December 2015
An Incompletely specified function is a Boolean function that only define output values for a subset of its inputs - i.e. a Boolean function whos output is a don't care for at least one of its input combinations. Incompletely specified functions often make no guarantees as to the unspecified output whatsoever.
Overview
| A | B | C | |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | X |
| 0 | 1 | 0 | X |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | X |
In many situations when working with combinational circuits, some combinations of inputs should not occur under normal working conditions. For circuits with such combinations, those combinations can be treated as either 0 or 1 depending on whichever yields a more simplified Boolean expression.
Boolean functions with don't care output terms are represented with a . For example consider the following function.
Which can be represented with the following truth table and K-map.
Note that depending on the final design of the circuit, the output for for example may be either 0 or 1.