(some organizing) |
|||
| (10 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | An '''adder''' (sometimes called a '''summer''') is a [[digital circuit]] | + | {{title|Adder}} |
| + | An '''adder''' (sometimes called a '''summer''') is a device that adds two numbers and generates the summed result. | ||
| + | |||
| + | In [[digital circuit]]s, an adder usually adds two ''N''-bit numbers and generates an ''N''-bit number. In addition to generating a sum, adders often also generate an [[overflow flag]] and a [[carry flag]]. Adders are used in many parts of the [[microprocessor]] such as the [[ALU]], [[program counter|PC]], [[counters]], calculating [[effective addresses]] and table indices, multipliers, filters, and in various other components. | ||
| + | |||
| + | In [[analog circuit]]s, [[adder (analog)|adders]] usually deal with two [[real number]]s instead. | ||
== Basic design == | == Basic design == | ||
| − | < | + | <math style="float:right;"> |
| − | + | \begin{align} | |
| − | A + B = Q \\ | + | A + B &= Q \\ |
| − | 0_2 + 0_2 = 00_2 \\ | + | 0_2 + 0_2 &= 00_2 \\ |
| − | 0_2 + 1_2 = 01_2 \\ | + | 0_2 + 1_2 &= 01_2 \\ |
| − | 1_2 + 0_2 = 01_2 \\ | + | 1_2 + 0_2 &= 01_2 \\ |
| − | 1_2 + 1_2 = 10_2 | + | 1_2 + 1_2 &= 10_2 \\ |
| + | \end{align} | ||
</math> | </math> | ||
| − | |||
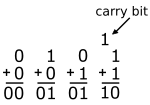
A 1-bit adder adds two single-bit values together. There are four such possible operations. All but the 1+1 operation result in a single-digit sum. The 1+1 operation produces a sum with two digits. The higher significant bit of that value is known as a carry. The digital component that performs the addition of two bits is called a '''half adder'''. When two multi-bit numbers are added together, the carry out from the lower bit must be accounted for in the higher addition of the higher bits. When a half adder accounts for a carry in, it becomes a '''full adder'''. | A 1-bit adder adds two single-bit values together. There are four such possible operations. All but the 1+1 operation result in a single-digit sum. The 1+1 operation produces a sum with two digits. The higher significant bit of that value is known as a carry. The digital component that performs the addition of two bits is called a '''half adder'''. When two multi-bit numbers are added together, the carry out from the lower bit must be accounted for in the higher addition of the higher bits. When a half adder accounts for a carry in, it becomes a '''full adder'''. | ||
=== Half Adders (HA) === | === Half Adders (HA) === | ||
{{main|Half adder}} | {{main|Half adder}} | ||
| − | |||
{| class="wikitable left" style="float:left; margin: 15px;" | {| class="wikitable left" style="float:left; margin: 15px;" | ||
!colspan="5"|Half Adder | !colspan="5"|Half Adder | ||
| Line 35: | Line 39: | ||
<math> | <math> | ||
| − | S = A \oplus B \\ | + | \begin{align} |
| − | C_{out} = A \cdot B | + | S =& A \oplus B \\ |
| + | C_{out} =& A \cdot B | ||
| + | \end{align} | ||
</math> | </math> | ||
| Line 42: | Line 48: | ||
=== Full Adder (FA) === | === Full Adder (FA) === | ||
{{main|full adder}} | {{main|full adder}} | ||
| − | |||
[[File:Full adder black box.svg|right|150px]] | [[File:Full adder black box.svg|right|150px]] | ||
A major drawback of a half adder is that it lacks the ability to add two bits and account for a carry-in that might have been brought from the previous digit. As previously stated, the carry-out of one half adder is the carry-in of the next half adder. A '''full adder''' is a simple device that can receive a carry-in bit input in addition to adding two single bit inputs. A full adder has three inputs A, B, and C<sub>in</sub> and two outputs S and C<sub>out</sub>. Full adders are typically combined together in a cascading way (C<sub>in</sub> to <sub>out</sub>), creating ''N''-bit adders (16, 32, 64, etc..). | A major drawback of a half adder is that it lacks the ability to add two bits and account for a carry-in that might have been brought from the previous digit. As previously stated, the carry-out of one half adder is the carry-in of the next half adder. A '''full adder''' is a simple device that can receive a carry-in bit input in addition to adding two single bit inputs. A full adder has three inputs A, B, and C<sub>in</sub> and two outputs S and C<sub>out</sub>. Full adders are typically combined together in a cascading way (C<sub>in</sub> to <sub>out</sub>), creating ''N''-bit adders (16, 32, 64, etc..). | ||
| Line 49: | Line 54: | ||
<math> | <math> | ||
| − | S = A \oplus B \oplus C \\ | + | \begin{align} |
| − | C_{out} = \text{ | + | S =& A \oplus B \oplus C \\ |
| + | C_{out} =& \text{Maj}(A, B, C) | ||
| + | \end{align} | ||
</math> | </math> | ||
| Line 84: | Line 91: | ||
===== Block carry-lookahead adder (BCLA) ===== | ===== Block carry-lookahead adder (BCLA) ===== | ||
{{main|Block carry-lookahead adder}} | {{main|Block carry-lookahead adder}} | ||
| + | {{empty section}} | ||
| + | |||
| + | ==== Ling adder ==== | ||
| + | {{main|Ling adder}} | ||
{{empty section}} | {{empty section}} | ||
| Line 105: | Line 116: | ||
{{main|Parallel-prefix adder}} | {{main|Parallel-prefix adder}} | ||
Parallel prefix adders are a class of highly-efficient binary adders. Several parallel-prefix adder topologies have been developed that exhibit various space and time characteristics. | Parallel prefix adders are a class of highly-efficient binary adders. Several parallel-prefix adder topologies have been developed that exhibit various space and time characteristics. | ||
| + | |||
| + | ===== Beaumont-Smith adder (BSA) ===== | ||
| + | {{main|Beaumont-Smith adder}} | ||
| + | {{empty section}} | ||
===== Ladner-Fischer adder ===== | ===== Ladner-Fischer adder ===== | ||
| Line 116: | Line 131: | ||
===== Brent-Kung adder ===== | ===== Brent-Kung adder ===== | ||
{{main|Brent-Kung adder}} | {{main|Brent-Kung adder}} | ||
| − | {{ | + | {{Brent-Kung adder is a very well-known logarithmic |
| + | adder architecture that gives an optimal number of stages from | ||
| + | input to all outputs but with asymmetric loading on all | ||
| + | intermediate stages. It is one of the parallel prefix adders. | ||
| + | Parallel prefix adders are unique class of adders that are based | ||
| + | on the use of generate and propagate signals. The cost and | ||
| + | wiring complexity is less in brent kung adders. But the gate | ||
| + | level depth of Brent-Kung adders is 0 (log2(n)), so the | ||
| + | speed is lower.}} | ||
===== Han-Carlson adder ===== | ===== Han-Carlson adder ===== | ||
| Line 123: | Line 146: | ||
=== Multi-operand adders === | === Multi-operand adders === | ||
| + | (Partial product accumulator) | ||
==== Carry-save adder array ==== | ==== Carry-save adder array ==== | ||
| Line 139: | Line 163: | ||
{{main|Overturned-stairs tree adder}} | {{main|Overturned-stairs tree adder}} | ||
{{empty section}} | {{empty section}} | ||
| + | |||
| + | ==== Compressors trees ==== | ||
| + | {{empty section}} | ||
| + | |||
| + | ===== 3:2 compressor tree ===== | ||
| + | {{main|3:2 compressor tree}} | ||
| + | {{empty section}} | ||
| + | |||
| + | ===== 4:2 compressor tree ===== | ||
| + | {{main|4:2 compressor tree}} | ||
| + | {{empty section}} | ||
| + | |||
| + | ===== Dadda tree ===== | ||
| + | {{main|Dadda tree}} | ||
| + | {{empty section}} | ||
| + | |||
| + | == See also == | ||
| + | * [[adder (analog)]] | ||
| + | |||
[[Category:Adders]] | [[Category:Adders]] | ||
Latest revision as of 08:01, 3 May 2016
An adder (sometimes called a summer) is a device that adds two numbers and generates the summed result.
In digital circuits, an adder usually adds two N-bit numbers and generates an N-bit number. In addition to generating a sum, adders often also generate an overflow flag and a carry flag. Adders are used in many parts of the microprocessor such as the ALU, PC, counters, calculating effective addresses and table indices, multipliers, filters, and in various other components.
In analog circuits, adders usually deal with two real numbers instead.
Contents
- 1 Basic design
- 2 BCD Adders
- 3 Advanced Designs
- 4 See also
Basic design[edit]
A 1-bit adder adds two single-bit values together. There are four such possible operations. All but the 1+1 operation result in a single-digit sum. The 1+1 operation produces a sum with two digits. The higher significant bit of that value is known as a carry. The digital component that performs the addition of two bits is called a half adder. When two multi-bit numbers are added together, the carry out from the lower bit must be accounted for in the higher addition of the higher bits. When a half adder accounts for a carry in, it becomes a full adder.
Half Adders (HA)[edit]
- Main article: Half adder
| Half Adder | ||||
|---|---|---|---|---|
| Input | Cout | S | Q10 | |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 2 |
A half adder is a simple device that adds two single bit inputs. The result of a half adder (in base 10) is either 0, 1, or 2. Two bits are required to represent that output; they are called the sum S and carry-out Cout. The carry-out of one half adder is typically used as the carry-in of the next half adder. For that reason it is said to have double the weight of the other bit.
The sum is 1 only when one of the operands is 1, otherwise it's 0. This can be realized by simply XORing them together. The carry out bit is one only when both addends are one; ANDing the two bits will generate the desired output.
Full Adder (FA)[edit]
- Main article: full adder
A major drawback of a half adder is that it lacks the ability to add two bits and account for a carry-in that might have been brought from the previous digit. As previously stated, the carry-out of one half adder is the carry-in of the next half adder. A full adder is a simple device that can receive a carry-in bit input in addition to adding two single bit inputs. A full adder has three inputs A, B, and Cin and two outputs S and Cout. Full adders are typically combined together in a cascading way (Cin to out), creating N-bit adders (16, 32, 64, etc..).
The sum output can be expressed as:
BCD Adders[edit]
- Main article: BCD Adder
Most adders typically use the binary numeral system, however they can use any other numerical representation such as binary-coded decimal. Binary adders are typically simpler to design when compared to a BCD adder where roughly 20 percent more circuitry is required.
Advanced Designs[edit]
Due to the adder's central role in so many digital circuits, it has been the subject of many researches. Various different designs have been developed over the years to meet a broad range of requirements (e.g. complexity, cost, space, and time trade-offs).
PGK Cell[edit]
| This section is empty; you can help add the missing info by editing this page. |
Many complex adder designs relay on the ability to calculate carry bits quickly.
Two-operand adders[edit]
Ripple-carry adder (RCA)[edit]
- Main article: Ripple-carry adder
| This section is empty; you can help add the missing info by editing this page. |
Carry-lookahead adder (CLA)[edit]
- Main article: Carry-lookahead adder
| This section is empty; you can help add the missing info by editing this page. |
Lookahead carry unit (LCU)[edit]
- Main article: Lookahead carry unit
| This section is empty; you can help add the missing info by editing this page. |
Ripple-block carry-lookahead adder (RCLA)[edit]
- Main article: Ripple-block carry-lookahead adder
| This section is empty; you can help add the missing info by editing this page. |
Block carry-lookahead adder (BCLA)[edit]
- Main article: Block carry-lookahead adder
| This section is empty; you can help add the missing info by editing this page. |
Ling adder[edit]
- Main article: Ling adder
| This section is empty; you can help add the missing info by editing this page. |
Manchester carry-chain adder[edit]
- Main article: Manchester carry-chain adder
| This section is empty; you can help add the missing info by editing this page. |
Carry-select adder[edit]
- Main article: Carry-select adder
| This section is empty; you can help add the missing info by editing this page. |
Carry-skip adder[edit]
- Main article: Carry-skip adder
| This section is empty; you can help add the missing info by editing this page. |
Conditional-Sum Adder[edit]
- Main article: Conditional-sum adder
| This section is empty; you can help add the missing info by editing this page. |
Parallel-prefix adders[edit]
- Main article: Parallel-prefix adder
Parallel prefix adders are a class of highly-efficient binary adders. Several parallel-prefix adder topologies have been developed that exhibit various space and time characteristics.
Beaumont-Smith adder (BSA)[edit]
- Main article: Beaumont-Smith adder
| This section is empty; you can help add the missing info by editing this page. |
Ladner-Fischer adder[edit]
- Main article: Ladner-Fischer adder
| This section is empty; you can help add the missing info by editing this page. |
Kogge-Stone adder[edit]
- Main article: Kogge-Stone adder
| This section is empty; you can help add the missing info by editing this page. |
Brent-Kung adder[edit]
- Main article: Brent-Kung adder
{{Brent-Kung adder is a very well-known logarithmic adder architecture that gives an optimal number of stages from input to all outputs but with asymmetric loading on all intermediate stages. It is one of the parallel prefix adders. Parallel prefix adders are unique class of adders that are based on the use of generate and propagate signals. The cost and wiring complexity is less in brent kung adders. But the gate level depth of Brent-Kung adders is 0 (log2(n)), so the speed is lower.}}
Han-Carlson adder[edit]
- Main article: Han-Carlson adder
| This section is empty; you can help add the missing info by editing this page. |
Multi-operand adders[edit]
(Partial product accumulator)
Carry-save adder array[edit]
- Main article: Carry-save adder array
| This section is empty; you can help add the missing info by editing this page. |
Wallace tree adder[edit]
- Main article: Wallace tree adder
| This section is empty; you can help add the missing info by editing this page. |
Balanced delay tree adder[edit]
- Main article: Balanced delay tree adder
| This section is empty; you can help add the missing info by editing this page. |
Overturned-stairs tree adder[edit]
- Main article: Overturned-stairs tree adder
| This section is empty; you can help add the missing info by editing this page. |
Compressors trees[edit]
| This section is empty; you can help add the missing info by editing this page. |
3:2 compressor tree[edit]
- Main article: 3:2 compressor tree
| This section is empty; you can help add the missing info by editing this page. |
4:2 compressor tree[edit]
- Main article: 4:2 compressor tree
| This section is empty; you can help add the missing info by editing this page. |
Dadda tree[edit]
- Main article: Dadda tree
| This section is empty; you can help add the missing info by editing this page. |