(added visual) |
|||
| Line 115: | Line 115: | ||
</math> | </math> | ||
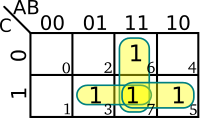
Each minterm in the equation is than transferred into the K-map where each variable in the minterm represents a 1 and each complemented variable represents a 0. | Each minterm in the equation is than transferred into the K-map where each variable in the minterm represents a 1 and each complemented variable represents a 0. | ||
| + | [[File:kmap example color coded (expression).svg|400px]] | ||
=== from truth table === | === from truth table === | ||
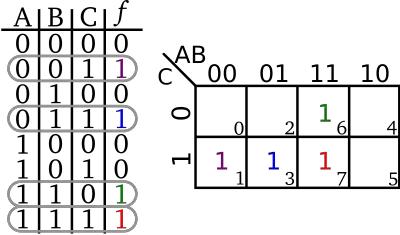
Transferring the data from a [[truth table]] to a K-map is slightly more straightforward since each cell corresponds directly to each row in the table. A cell on the K-map is labeled 1 when the row they represent in the truth table results in a 1; otherwise the cell is labeled 0. Often times if the cell is 0, the 0 itself is simply omitted and is understood to mean that. | Transferring the data from a [[truth table]] to a K-map is slightly more straightforward since each cell corresponds directly to each row in the table. A cell on the K-map is labeled 1 when the row they represent in the truth table results in a 1; otherwise the cell is labeled 0. Often times if the cell is 0, the 0 itself is simply omitted and is understood to mean that. | ||
| + | [[File:kmap example color coded (table).svg|400px]] | ||
Revision as of 12:35, 10 December 2015
3-input MAJ gate
Marnaugh Map (K-map) is a graphical tool that provides a simple and straightforward method of minimizing Boolean expressions. The K-map method was introduced in 1953 by Maurice Karnaugh as an enhancement to Veitch diagram.
Contents
Map Construction
Map Formats
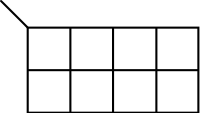
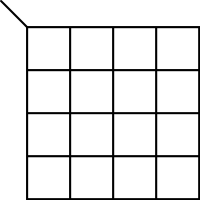
A K-map is a square or rectangle divided into a number of smaller squares called cells. Each cell on the K-Map corresponds directly to a line in a truth table. There are always cells in a K-Map where is the number of variables in the function. Below are the usual formats for 1-4 variable k-maps (larges k-maps are discussed later on).
| 1-Variable K-map | 2-Variables K-map |
|---|---|
 |
|
| 3-Variables K-map | 4-Variables K-map |
 |
|
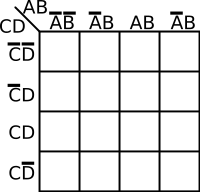
Map Labeling
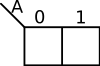
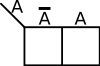
The coordinates of the cells in a K-map are the input value combinations from the truth table. There are a number of common ways to label a K-map. The two most common methods are numerically and by variables and their complements. There are advantages to both. Regardless of which way you choose, the coordinates of two adjacent cells differ by only one variable - i.e. only one 0 can switch to a 1 and vice versa between two adjacent cells. For example, consider a function with 2 variables, the order by which you list them would be . Note how 11 and 10 were switched so that only one value is different.
| Numerically | Variables |
|---|---|
| 1-Variable K-map | |
 |
|
| 2-Variables K-map | |
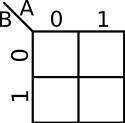 |
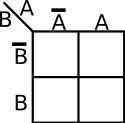
|
| 3-Variables K-map | |
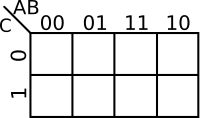 |

|
| 4-Variables K-map | |
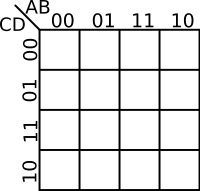 |
|
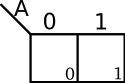
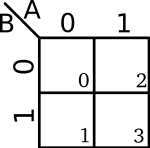
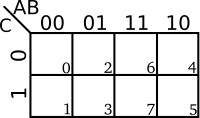
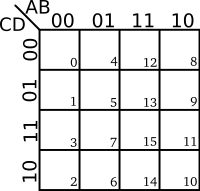
Map Cell Numbering
| Inputs | Minterms | Maxterms | ||||
|---|---|---|---|---|---|---|
| A | B | Minterms | Index | Maxterms | Index | |
| 0 | 0 | |||||
| 0 | 1 | |||||
| 1 | 0 | |||||
| 1 | 1 | |||||
| A | B | C | Minterms | Index | Maxterms | Index |
| 0 | 0 | 0 | ||||
| 0 | 0 | 1 | ||||
| 0 | 1 | 0 | ||||
| 0 | 1 | 1 | ||||
| 1 | 0 | 0 | ||||
| 1 | 0 | 1 | ||||
| 1 | 1 | 0 | ||||
| 1 | 1 | 1 | ||||
Sometimes the individual cells are numbered in accordance with their minterm and maxterm indices. Strictly speaking this is unnecessary, but it may be useful in various situations when working with minterms and maxterms. Cell numbering are usually written in one of the cell corners.
| 1-Variable K-map | 2-Variables K-map |
|---|---|
 |
|
| 3-Variables K-map | 4-Variables K-map |
 |
|
Populating a K-map
Populating a K-map can be done with a Boolean expression or a truth table.
from Boolean expression
Because each cell on the K-map represents a particular minterm (or maxterm). Converting the desired Boolean function into sum of minterms form can help considerably.
Consider the following Boolean function.
To make it easier to transfer the data to a K-map, the equation can be manipulated a bit so that it's in sum of minterms canonical form.
Each minterm in the equation is than transferred into the K-map where each variable in the minterm represents a 1 and each complemented variable represents a 0.
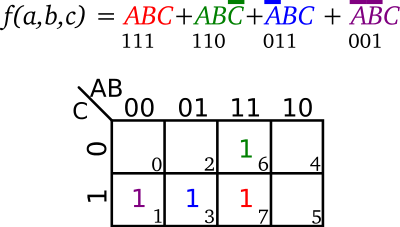
from truth table
Transferring the data from a truth table to a K-map is slightly more straightforward since each cell corresponds directly to each row in the table. A cell on the K-map is labeled 1 when the row they represent in the truth table results in a 1; otherwise the cell is labeled 0. Often times if the cell is 0, the 0 itself is simply omitted and is understood to mean that.