From WikiChip
Difference between revisions of "karnaugh map"

(→‎Map Cell Numbering: +images +table)
(Fix typo)
 
(21 intermediate revisions by 8 users not shown)
Line 1: Line 1:
 
{{title|Karnaugh Map (K-map)}}
 
{{title|Karnaugh Map (K-map)}}
−
<div style="float: right; text-align: center; margin: 20px; width: 250px">
+
<div style="float: right; text-align: center; margin: 20px; width: 250px">[[File:3-input MAJ gate kmap.svg|200px]]<br />3-input [[MAJ]] gate<br /><math>
−
[[File:3-input MAJ gate kmap.svg|200px]]<br />
 
−
3-input [[MAJ]] gate<br />
 
−
<math>
 
 
\begin{align}
 
\begin{align}
 
f(a,b,c) =& AB+AC+BC \\
 
f(a,b,c) =& AB+AC+BC \\
 
         =& \sum m(3,5,6,7) \\
 
         =& \sum m(3,5,6,7) \\
−
f^\prime(a,b,c) =& \prod M(0,1,2,4)
+
f(a,b,c) =& \prod M(0,1,2,4)
 
\end{align}
 
\end{align}
 
</math>
 
</math>
 
</div>
 
</div>
−
'''Marnaugh Map''' ('''K-map''') is a graphical tool that provides a simple and straightforward method of [[logic minimization|minimizing]] [[Boolean algebra|Boolean expressions]]. The K-map method was introduced in 1953 by [[Maurice Karnaugh]] as an enhancement to [[Veitch diagram]].
+
'''Karnaugh Map''' ('''K-map''') (pronounced ''car-no map'') is a graphical tool that provides a simple and straightforward method of [[logic minimization|minimizing]] [[Boolean algebra|Boolean expressions]]. The K-map method was introduced in 1953 by [[Maurice Karnaugh]] as an enhancement to [[Veitch diagram]].
  
−
== Format ==
+
== Map Construction ==
 
=== Map Formats ===
 
=== Map Formats ===
 
A K-map is a square or rectangle divided into a number of smaller squares called '''cells'''. Each cell on the K-Map corresponds directly to a line in a [[truth table]]. There are always <math>2^n</math> cells in a K-Map where <math>n</math> is the number of variables in the {{ba|function}}. Below are the usual formats for 1-4 variable k-maps (larges k-maps are discussed later on).
 
A K-map is a square or rectangle divided into a number of smaller squares called '''cells'''. Each cell on the K-Map corresponds directly to a line in a [[truth table]]. There are always <math>2^n</math> cells in a K-Map where <math>n</math> is the number of variables in the {{ba|function}}. Below are the usual formats for 1-4 variable k-maps (larges k-maps are discussed later on).
Line 94: Line 91:
 
| [[File:kmap (numbering) (3 vars).svg|200px]] || [[File:kmap (numbering) (4 vars).svg|200px]]
 
| [[File:kmap (numbering) (3 vars).svg|200px]] || [[File:kmap (numbering) (4 vars).svg|200px]]
 
|}
 
|}
 +
 +
== Populating a K-map==
 +
Populating a K-map can be done with a [[boolean algebra|Boolean expression]] or a [[truth table]].
 +
=== from Boolean expression ===
 +
Because each cell on the K-map represents a particular [[minterm]] (or [[maxterm]]). Converting the desired [[Boolean function]] into [[sum of minterms]] form can help considerably.
 +
 +
Consider the following [[Boolean function]].
 +
::<math>f(A,B,C) = \bar A C + B(A+C)</math>
 +
To make it easier to transfer the data to a K-map, the equation can be manipulated a bit so that it's in [[sum of minterms]] canonical form.
 +
::<math>
 +
\begin{align}
 +
f(A,B,C) =& \bar A C + B(A+C) \\
 +
        =& AB + \bar AC + BC && \mbox{By Distributive Axiom} \\
 +
        =& AB(C+\bar C) + \bar AC(B+\bar B) + BC(A+\bar A) && \because (X+\bar X) = 1 \mbox{ By Inverse Axiom} \\
 +
        =& ABC+AB\bar C+ \bar ACB + \bar AC\bar B + BCA + BC \bar A && \mbox{ By Distributive Axiom} \\
 +
        =& ABC+AB\bar C+ \bar ABC + \bar A\bar BC + ABC + \bar ABC && \mbox{ By Commutative Axiom} \\
 +
        =& ABC+AB\bar C+ \bar ABC + \bar A\bar BC && \mbox{ By Idempotent Law} \\
 +
        =& m_7 + m_6 + m_3 + m_1
 +
\end{align}
 +
</math>
 +
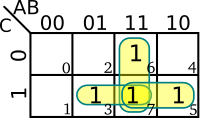
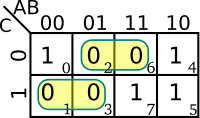
Each minterm in the equation is then transferred into the K-map where each variable in the minterm represents a 1 and each complemented variable represents a 0.
 +
[[File:kmap example color coded (expression).svg|400px]]
 +
=== from truth table ===
 +
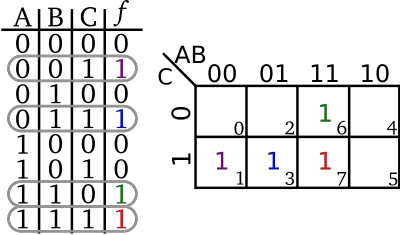
Transferring the data from a [[truth table]] to a K-map is slightly more straightforward since each cell corresponds directly to each row in the table. A cell on the K-map is labeled 1 when the row they represent in the truth table results in a 1; otherwise the cell is labeled 0. Often times if the cell is 0, the 0 itself is simply omitted and is understood to mean that.
 +
 +
[[File:kmap example color coded (table).svg|400px]]
 +
==Simplification==
 +
Generating simplified equations for a Karnaugh map involves two simple steps:
 +
#finding largest groups of 1s
 +
#generating an equation from the identified groups
 +
[[File:kmap terms.svg|400px|right]]
 +
===Groups===
 +
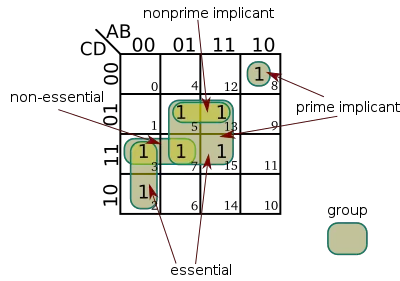
An '''[[implicant]]''' is the individual product term in the [[sum of product]] expression. On a K-map implicants are represented as one or more adjacent cells of 1s. A '''group''' is a loose term for the enclosure containing adjacent squares of 1s. When a group contains the most adjacent 1 cells it possibly can, it is called a '''[[prime implicant]]'''. When a group encloses cells of 1s that are not shared with any other group, it is called an '''[[essential prime implicant]]'''. Likewise, when a group encloses cells of 1s that are all shared with other groups, it is called a '''[[non-essential prime implicant]]'''.
 +
====Rules====
 +
When grouping implicants together, there is a set of rules that must be followed:
 +
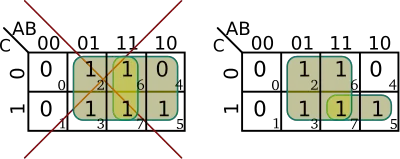
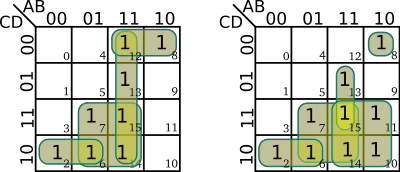
* Groups are made of power of 2 number of cells (e.g. 1, 2, 4, 8, 16)
 +
::[[File:kmap rules - powers of 2.svg|400px]]
 +
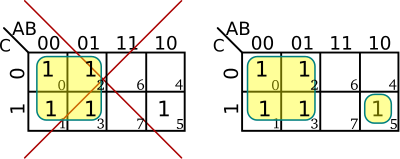
* Groups consists of one or more cells of 1s only - i.e. no cells of 0s
 +
::[[File:kmap rules - only 1s.svg|400px]]
 +
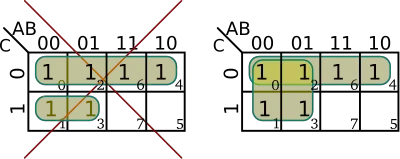
* Every cell of 1 must be in at lest one group
 +
::[[File:kmap rules - no leftout cells.svg|400px]]
 +
* Overlapping groups are allowed
 +
::[[File:kmap rules - overlapping allowed.svg|400px]]
 +
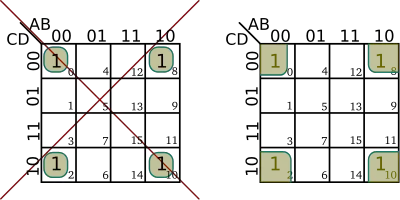
* Wrapping around is allowed
 +
::[[File:kmap rules - wrapping around.svg|400px]]
 +
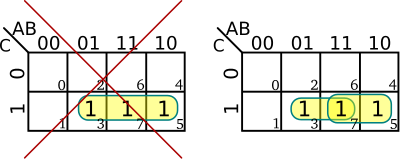
* Groups can be made of cells that are adjacent to one another. I.e. cells must be alongside, above or below one another
 +
::[[File:kmap rules - adjacent cells.svg|400px]]
 +
* Groups may not go diagonally
 +
::[[File:kmap rules - no diagonals.svg|400px]]
 +
* Groups should be large as possible.
 +
::[[File:kmap rules - largest groups.svg|400px]]
 +
===Simplified Equation===
 +
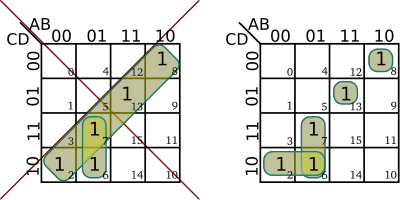
After all the maximum groups have been marked in the K-map, a simplified Boolean expression may be obtained by ORing together the individual expressions for each of the groups. The expression for a group is the variables or the complement of the variables that do not change between cells.
 +
 +
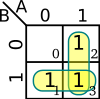
[[File:kmap example 1.svg|left|150px]]
 +
For example, consider the example to the left. This Karnaugh map has a single group that covers both <math>B = 0</math> and <math>B = 1</math>. Because <math>B</math> changes, it is dropped from our expression, living us with just <math>A = 1</math>. Therefore the Boolean expression for this K-map is simply <math>f(A,B) = \sum m(2,3) = A</math>.
 +
 +
[[File:kmap example 2.svg|right|100px]]
 +
The Karnaugh map on the right on the other hand has two groups. One group spans both <math>B = 0</math> and <math>B = 1</math> and another that spans <math>A = 0</math> and <math>A = 1</math>. In the expression for the group that spans vertically, <math>B</math> changes yielding the expression <math>A</math>. Likewise in the expression that spans horizontally, <math>A</math> changes, yielding the expression <math>B</math>. The simplified equation for this K-map is the ORing of all the individual term - <math>f(A,B) = \sum m(1,2,3) = A+B</math>.
 +
 +
 +
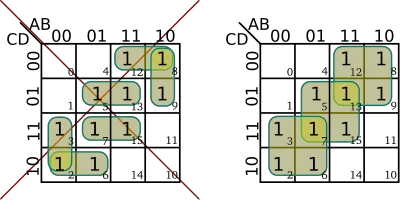
[[File:kmap example 3.svg|left|200px]]
 +
In this K-map, cells 0 and 4 are considered adjacent as well as cells 3 and 7. For the group involving cells 0 and 4, <math>A</math> changes, therefore it is dropped from the expression. Because <math>B</math> is always 0 and <math>C</math> is always 0 as well, the equation for that group is <math>\bar B \bar C</math>. For the second group involving cells 3 and 7,  <math>A</math> changes once again. In this group <math>B</math> is always 1 and <math>C</math> is always 1 as well. The equation for this group is <math>BC</math>. The final simplified equation for this K-map is the ORing of all the terms - <math>f(A,B,C) = \sum m(0,3,4,7) = \bar B \bar C + BC</math>.
 +
{{clear}}
 +
== Don't cares ==
 +
{{further|don't care}}
 +
{| class="wikitable" style="float: right; text-align: center;"
 +
! A !! B !! C !! Q
 +
|-
 +
| 0 || 0 || 0 || {{X}}
 +
|-
 +
| 0 || 0 || 1 || {{X}}
 +
|-
 +
| 0 || 1 || 0 || 0
 +
|-
 +
| 0 || 1 || 1 || 0
 +
|-
 +
| 1 || 0 || 0 || 1
 +
|-
 +
| 1 || 0 || 1 || 1
 +
|-
 +
| 1 || 1 || 0 || 0
 +
|-
 +
| 1 || 1 || 1 || 1
 +
|}
 +
[[Incompletely specified function]] are functions with combination of inputs that should never occur. Those unspecified [[minterm]]s are called [[don't care]] values. Don't care values open opportunities for further simplification of the Boolean expression. When it comes to Karnaugh maps, don't care values, which are represented with ''X'''s are considered either a 0 or 1, whichever results in the biggest group - i.e. the simplest expression.
 +
 +
[[File:kmap (don't care example).svg|left|200px]]
 +
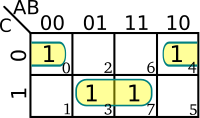
The [[truth table]] to the Karnaugh map below is on the right and represents an [[incompletely specified function]]. Note the don't care values for two of the outputs. I.e. <math>f(0,0,0)</math> and <math>f(0,0,1)</math> should never happen. In this example, the two don't care values can be used to make the 2-cell group be a 4-cell group allowing us to eliminate a whole variable: <math>A</math>. The Boolean expression is therefore <math>f(a,b,c) = \bar B + AC</math>.
 +
{{clear}}
 +
 +
== Product of Sum (PoS)==
 +
[[File:kmap pos example.svg|200px|right]]
 +
While usually used to generate sum of products, Karnaugh maps can be used to generate [[product of sum]] just as easily by applying the same rules we designed above, but for 0 cells instead. Remember that when working with [[maxterm]]s instead of [[minterm]]s, when a variable is 1, it is complemented instead of when it's 0.
 +
 +
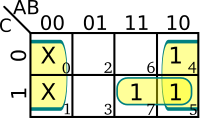
For example consider the K-map on the right. In this case the 0 cells are grouped. The Boolean function for this Karnaugh map is
 +
::<math>f(A,B,C) = \prod M(2,6,1,3) = (\bar B+C)(A+\bar C)</math>.
 +
{{clear}}
 +
== Hazard analysis ==
 +
{{empty section}}
 +
 +
== Larger Karnaugh Maps==
 +
{{empty section}}
 +
=== 5-variable K-map===
 +
{{empty section}}
 +
 +
=== 6-variable K-map===
 +
{{empty section}}
 +
 +
== Examples ==
 +
{{empty section}}
 +
 +
== See also ==
 +
* [[Boolean algebra]]

Latest revision as of 23:21, 5 September 2019

3-input MAJ gate kmap.svg
3-input MAJ gate
Equation StartLayout 1st Row 1st Column f left-parenthesis a comma b comma c right-parenthesis equals 2nd Column upper A upper B plus upper A upper C plus upper B upper C 2nd Row 1st Column equals 2nd Column sigma-summation m left-parenthesis 3 comma 5 comma 6 comma 7 right-parenthesis 3rd Row 1st Column f left-parenthesis a comma b comma c right-parenthesis equals 2nd Column product upper M left-parenthesis 0 comma 1 comma 2 comma 4 right-parenthesis EndLayout

Karnaugh Map (K-map) (pronounced car-no map) is a graphical tool that provides a simple and straightforward method of minimizing Boolean expressions. The K-map method was introduced in 1953 by Maurice Karnaugh as an enhancement to Veitch diagram.

Map Construction[edit]

Map Formats[edit]

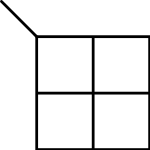
A K-map is a square or rectangle divided into a number of smaller squares called cells. Each cell on the K-Map corresponds directly to a line in a truth table. There are always Equation 2 Superscript n cells in a K-Map where Equation n is the number of variables in the function. Below are the usual formats for 1-4 variable k-maps (larges k-maps are discussed later on).

1-Variable K-map 2-Variables K-map
kmap (no labels) (1 var).svg kmap (no labels) (2 vars).svg
3-Variables K-map 4-Variables K-map
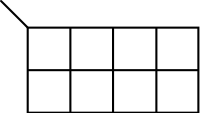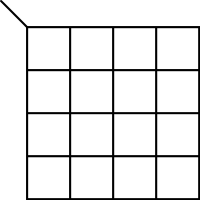
kmap (no labels) (3 vars).svg kmap (no labels) (4 vars).svg

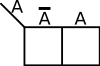
Map Labeling[edit]

The coordinates of the cells in a K-map are the input value combinations from the truth table. There are a number of common ways to label a K-map. The two most common methods are numerically and by variables and their complements. There are advantages to both. Regardless of which way you choose, the coordinates of two adjacent cells differ by only one variable - i.e. only one 0 can switch to a 1 and vice versa between two adjacent cells. For example, consider a function with 2 variables, the order by which you list them would be Equation 00 comma 01 comma 11 comma 10 . Note how 11 and 10 were switched so that only one value is different.

Numerically Variables
1-Variable K-map
kmap (1 var).svg kmap (labels) (1 var).svg
2-Variables K-map
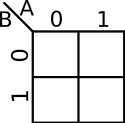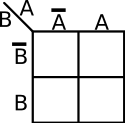
kmap (2 vars).svg kmap (labels) (2 vars).svg
3-Variables K-map
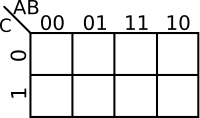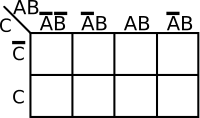
kmap (3 vars).svg kmap (labels) (3 vars).svg
4-Variables K-map
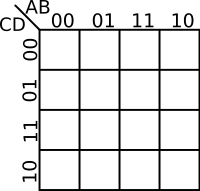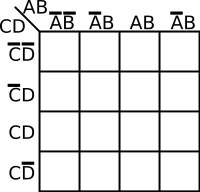
kmap (4 vars).svg kmap (labels) (4 vars).svg

Map Cell Numbering[edit]

Inputs Minterms Maxterms
A B Minterms Index Maxterms Index
0 0 Equation upper A overbar upper B overbar Equation m 0 Equation upper A plus upper B Equation upper M 0
0 1 Equation upper A overbar upper B Equation m 1 Equation upper A plus upper B overbar Equation upper M 1
1 0 Equation upper A upper B overbar Equation m 2 Equation upper A overbar plus upper B Equation upper M 2
1 1 Equation upper A upper B Equation m 3 Equation upper A overbar plus upper B overbar Equation upper M 3
A B C Minterms Index Maxterms Index
0 0 0 Equation upper A overbar upper B overbar upper C overbar Equation m 0 Equation upper A plus upper B plus upper C Equation upper M 0
0 0 1 Equation upper A overbar upper B overbar upper C Equation m 1 Equation upper A plus upper B plus upper C overbar Equation upper M 1
0 1 0 Equation upper A overbar upper B upper C overbar Equation m 2 Equation upper A plus upper B overbar plus upper C Equation upper M 2
0 1 1 Equation upper A overbar upper B upper C Equation m 3 Equation upper A plus upper B overbar plus upper C overbar Equation upper M 3
1 0 0 Equation upper A upper B overbar upper C overbar Equation m 4 Equation upper A overbar plus upper B plus upper C Equation upper M 4
1 0 1 Equation upper A upper B overbar upper C Equation m 5 Equation upper A overbar plus upper B plus upper C overbar Equation upper M 5
1 1 0 Equation upper A upper B upper C overbar Equation m 6 Equation upper A plus upper B plus upper C overbar Equation upper M 6
1 1 1 Equation upper A upper B upper C Equation m 7 Equation upper A overbar plus upper B overbar plus upper C overbar Equation upper M 7

Sometimes the individual cells are numbered in accordance with their minterm and maxterm indices. Strictly speaking this is unnecessary, but it may be useful in various situations when working with minterms and maxterms. Cell numbering are usually written in one of the cell corners.

1-Variable K-map 2-Variables K-map
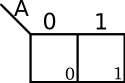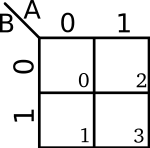
kmap (numbering) (1 var).svg kmap (numbering) (2 vars).svg
3-Variables K-map 4-Variables K-map
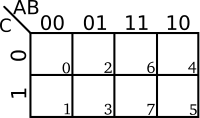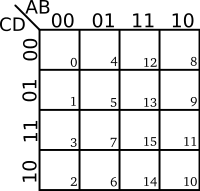
kmap (numbering) (3 vars).svg kmap (numbering) (4 vars).svg

Populating a K-map[edit]

Populating a K-map can be done with a Boolean expression or a truth table.

from Boolean expression[edit]

Because each cell on the K-map represents a particular minterm (or maxterm). Converting the desired Boolean function into sum of minterms form can help considerably.

Consider the following Boolean function.

Equation f left-parenthesis upper A comma upper B comma upper C right-parenthesis equals upper A overbar upper C plus upper B left-parenthesis upper A plus upper C right-parenthesis

To make it easier to transfer the data to a K-map, the equation can be manipulated a bit so that it's in sum of minterms canonical form.

Equation StartLayout 1st Row 1st Column f left-parenthesis upper A comma upper B comma upper C right-parenthesis equals 2nd Column upper A overbar upper C plus upper B left-parenthesis upper A plus upper C right-parenthesis 2nd Row 1st Column equals 2nd Column upper A upper B plus upper A overbar upper C plus upper B upper C 3rd Column Blank 4th Column By Distributive Axiom 3rd Row 1st Column equals 2nd Column upper A upper B left-parenthesis upper C plus upper C overbar right-parenthesis plus upper A overbar upper C left-parenthesis upper B plus upper B overbar right-parenthesis plus upper B upper C left-parenthesis upper A plus upper A overbar right-parenthesis 3rd Column Blank 4th Column because left-parenthesis upper X plus upper X overbar right-parenthesis equals 1 By Inverse Axiom 4th Row 1st Column equals 2nd Column upper A upper B upper C plus upper A upper B upper C overbar plus upper A overbar upper C upper B plus upper A overbar upper C upper B overbar plus upper B upper C upper A plus upper B upper C upper A overbar 3rd Column Blank 4th Column By Distributive Axiom 5th Row 1st Column equals 2nd Column upper A upper B upper C plus upper A upper B upper C overbar plus upper A overbar upper B upper C plus upper A overbar upper B overbar upper C plus upper A upper B upper C plus upper A overbar upper B upper C 3rd Column Blank 4th Column By Commutative Axiom 6th Row 1st Column equals 2nd Column upper A upper B upper C plus upper A upper B upper C overbar plus upper A overbar upper B upper C plus upper A overbar upper B overbar upper C 3rd Column Blank 4th Column By Idempotent Law 7th Row 1st Column equals 2nd Column m 7 plus m 6 plus m 3 plus m 1 EndLayout

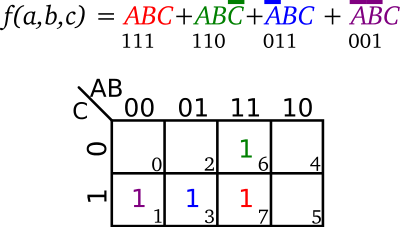
Each minterm in the equation is then transferred into the K-map where each variable in the minterm represents a 1 and each complemented variable represents a 0. kmap example color coded (expression).svg

from truth table[edit]

Transferring the data from a truth table to a K-map is slightly more straightforward since each cell corresponds directly to each row in the table. A cell on the K-map is labeled 1 when the row they represent in the truth table results in a 1; otherwise the cell is labeled 0. Often times if the cell is 0, the 0 itself is simply omitted and is understood to mean that.

kmap example color coded (table).svg

Simplification[edit]

Generating simplified equations for a Karnaugh map involves two simple steps:

  1. finding largest groups of 1s
  2. generating an equation from the identified groups
kmap terms.svg

Groups[edit]

An implicant is the individual product term in the sum of product expression. On a K-map implicants are represented as one or more adjacent cells of 1s. A group is a loose term for the enclosure containing adjacent squares of 1s. When a group contains the most adjacent 1 cells it possibly can, it is called a prime implicant. When a group encloses cells of 1s that are not shared with any other group, it is called an essential prime implicant. Likewise, when a group encloses cells of 1s that are all shared with other groups, it is called a non-essential prime implicant.

Rules[edit]

When grouping implicants together, there is a set of rules that must be followed:

  • Groups are made of power of 2 number of cells (e.g. 1, 2, 4, 8, 16)
kmap rules - powers of 2.svg
  • Groups consists of one or more cells of 1s only - i.e. no cells of 0s
kmap rules - only 1s.svg
  • Every cell of 1 must be in at lest one group
kmap rules - no leftout cells.svg
  • Overlapping groups are allowed
kmap rules - overlapping allowed.svg
  • Wrapping around is allowed
kmap rules - wrapping around.svg
  • Groups can be made of cells that are adjacent to one another. I.e. cells must be alongside, above or below one another
kmap rules - adjacent cells.svg
  • Groups may not go diagonally
kmap rules - no diagonals.svg
  • Groups should be large as possible.
kmap rules - largest groups.svg

Simplified Equation[edit]

After all the maximum groups have been marked in the K-map, a simplified Boolean expression may be obtained by ORing together the individual expressions for each of the groups. The expression for a group is the variables or the complement of the variables that do not change between cells.

kmap example 1.svg

For example, consider the example to the left. This Karnaugh map has a single group that covers both Equation upper B equals 0 and Equation upper B equals 1 . Because Equation upper B changes, it is dropped from our expression, living us with just Equation upper A equals 1 . Therefore the Boolean expression for this K-map is simply Equation f left-parenthesis upper A comma upper B right-parenthesis equals sigma-summation m left-parenthesis 2 comma 3 right-parenthesis equals upper A .

kmap example 2.svg

The Karnaugh map on the right on the other hand has two groups. One group spans both Equation upper B equals 0 and Equation upper B equals 1 and another that spans Equation upper A equals 0 and Equation upper A equals 1 . In the expression for the group that spans vertically, Equation upper B changes yielding the expression Equation upper A . Likewise in the expression that spans horizontally, Equation upper A changes, yielding the expression Equation upper B . The simplified equation for this K-map is the ORing of all the individual term - Equation f left-parenthesis upper A comma upper B right-parenthesis equals sigma-summation m left-parenthesis 1 comma 2 comma 3 right-parenthesis equals upper A plus upper B .


kmap example 3.svg

In this K-map, cells 0 and 4 are considered adjacent as well as cells 3 and 7. For the group involving cells 0 and 4, Equation upper A changes, therefore it is dropped from the expression. Because Equation upper B is always 0 and Equation upper C is always 0 as well, the equation for that group is Equation upper B overbar upper C overbar . For the second group involving cells 3 and 7, Equation upper A changes once again. In this group Equation upper B is always 1 and Equation upper C is always 1 as well. The equation for this group is Equation upper B upper C . The final simplified equation for this K-map is the ORing of all the terms - Equation f left-parenthesis upper A comma upper B comma upper C right-parenthesis equals sigma-summation m left-parenthesis 0 comma 3 comma 4 comma 7 right-parenthesis equals upper B overbar upper C overbar plus upper B upper C .

Don't cares[edit]

Further information: don't care
A B C Q
0 0 0 X
0 0 1 X
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 0
1 1 1 1

Incompletely specified function are functions with combination of inputs that should never occur. Those unspecified minterms are called don't care values. Don't care values open opportunities for further simplification of the Boolean expression. When it comes to Karnaugh maps, don't care values, which are represented with X's are considered either a 0 or 1, whichever results in the biggest group - i.e. the simplest expression.

kmap (don't care example).svg

The truth table to the Karnaugh map below is on the right and represents an incompletely specified function. Note the don't care values for two of the outputs. I.e. Equation f left-parenthesis 0 comma 0 comma 0 right-parenthesis and Equation f left-parenthesis 0 comma 0 comma 1 right-parenthesis should never happen. In this example, the two don't care values can be used to make the 2-cell group be a 4-cell group allowing us to eliminate a whole variable: Equation upper A . The Boolean expression is therefore Equation f left-parenthesis a comma b comma c right-parenthesis equals upper B overbar plus upper A upper C .

Product of Sum (PoS)[edit]

kmap pos example.svg

While usually used to generate sum of products, Karnaugh maps can be used to generate product of sum just as easily by applying the same rules we designed above, but for 0 cells instead. Remember that when working with maxterms instead of minterms, when a variable is 1, it is complemented instead of when it's 0.

For example consider the K-map on the right. In this case the 0 cells are grouped. The Boolean function for this Karnaugh map is

Equation f left-parenthesis upper A comma upper B comma upper C right-parenthesis equals product upper M left-parenthesis 2 comma 6 comma 1 comma 3 right-parenthesis equals left-parenthesis upper B overbar plus upper C right-parenthesis left-parenthesis upper A plus upper C overbar right-parenthesis .

Hazard analysis[edit]

New text document.svg This section is empty; you can help add the missing info by editing this page.

Larger Karnaugh Maps[edit]

New text document.svg This section is empty; you can help add the missing info by editing this page.

5-variable K-map[edit]

New text document.svg This section is empty; you can help add the missing info by editing this page.

6-variable K-map[edit]

New text document.svg This section is empty; you can help add the missing info by editing this page.

Examples[edit]

New text document.svg This section is empty; you can help add the missing info by editing this page.

See also[edit]

Retrieved from "https://en.wikichip.org/w/index.php?title=karnaugh_map&oldid=93493"