(→Equation) |
(Improve grammar) |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 9: | Line 9: | ||
</math> | </math> | ||
| − | The total execution time, <math>T_\text{exec}</math>, required to execute a specific finite program is. | + | The total [[execution time]], <math>T_\text{exec}</math>, required to execute a specific finite program is. |
| − | :<math>T_\text{exec} = \frac{\texttt{IC} \times \texttt{CPI}}{f} \qquad \qquad [\texttt{seconds}]</math> | + | :<math>T_\text{exec} = \frac{\texttt{IC} \times \texttt{CPI}}{f} \qquad \qquad [\frac{\texttt{seconds}}{\texttt{program}}]</math> |
Where, | Where, | ||
| Line 47: | Line 47: | ||
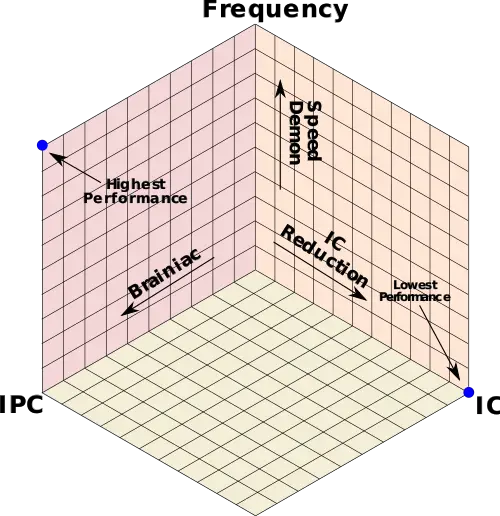
:[[File:cpu perf graph.svg|500px]] | :[[File:cpu perf graph.svg|500px]] | ||
| + | |||
| + | Although in theory, the best performance can be achieved through very [[clock speed|high frequency]] and very high [[IPC]], in practice the design requirements for the two are largely contradictory. Achieving higher IPC requires higher logic circuit complexity. This significantly reduces the working frequency range. Likewise, by reducing the logic circuitry complexity, it's possible to increases the frequency at expense of the IPC. Both knobs are also affected by the [[process technology]] that is used to manufacture the design. In general, smaller nodes allows for slightly more complexity without regressing frequency (the exact impact is very node-dependent). Thus achieving a good performance requires a good balance between IPC, frequency, and the instruction count. | ||
Latest revision as of 16:58, 10 February 2023
The performance of a microprocessor is a measure of its efficiency in terms of the amount of useful work it accomplishes.
Equation[edit]
The performance (time-to-execute) of a certain finite workload is the reciprocal of execution time.
The total execution time, , required to execute a specific finite program is.
Where,
- IC is the instruction count
- CPI (), the average cycles per instructions.
- is the clock speed
Thus, the performance of a microprocessor can also be defined as.
Note that for the sake of brevity, sometimes the instruction count is omitted when referring to the performance of a fixed portion of code. In other words, when the instruction count is fixed because the program is not being recompiled, it is sometimes omitted from the equation. However, doing this ignores the fact that recompiling code can have a positive impact on performance.
Three Performance Knobs[edit]
With the performance equation from above.
It can be seen that there are three control knobs for improving performance:
- Frequency - Increasing the frequency, thus reducing the length of each clock cycle. Architectures that take this approach are referred to as a speed demon design.
- IPC - Increasing the instruction throughput by exploiting more instruction-level parallelism. Architectures that take this approach are referred to as a brainiac design.
- Instruction Count - Reducing the instruction count, thus reducing the total amount of work that needs to be completed. This can be done through new compiler optimizations or through the introduction of new instruction set extensions.
Often times, a combination of all three is necessary to achieve good performance and power efficiency balance.
Although in theory, the best performance can be achieved through very high frequency and very high IPC, in practice the design requirements for the two are largely contradictory. Achieving higher IPC requires higher logic circuit complexity. This significantly reduces the working frequency range. Likewise, by reducing the logic circuitry complexity, it's possible to increases the frequency at expense of the IPC. Both knobs are also affected by the process technology that is used to manufacture the design. In general, smaller nodes allows for slightly more complexity without regressing frequency (the exact impact is very node-dependent). Thus achieving a good performance requires a good balance between IPC, frequency, and the instruction count.