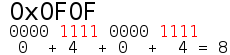(→Software support) |
(→Implementations) |
||
| Line 10: | Line 10: | ||
int popcount(unsigned x) | int popcount(unsigned x) | ||
{ | { | ||
| − | int c; | + | int c = 0; |
| − | for ( | + | for (; x != 0; x >>= 1) |
if (x & 1) | if (x & 1) | ||
c++; | c++; | ||
| Line 37: | Line 37: | ||
{ | { | ||
return popcount(num & 0xFFFF) + popcount(num >> 16); | return popcount(num & 0xFFFF) + popcount(num >> 16); | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | A more advanced algorithm that is also quicker, combining subtraction and bitwise AND: | ||
| + | |||
| + | <source lang="c"> | ||
| + | int popcount(unsigned x) | ||
| + | { | ||
| + | int c = 0; | ||
| + | for (; x != 0; x &= x - 1) | ||
| + | c++; | ||
| + | return c; | ||
} | } | ||
</source> | </source> | ||
Revision as of 12:33, 4 December 2019
The population count (or popcount) of a specific value is the number of set bits in that value. For example, the population count of 0F0F16, 111116, and 0016 are 810, 410, and 010 respectively.
Calculating the population count efficiently has been widely studied with implementations existing for both software and hardware. Many of the popular microprocessors also provide hardware support for this operation.
Implementations
The most basic implementation of a population count function as described in K&R can be written as
int popcount(unsigned x)
{
int c = 0;
for (; x != 0; x >>= 1)
if (x & 1)
c++;
return c;
}
If a large amount of memory is allowed to be used, one can precompile a large lookup table of population count and simply lookup the value from there every time. For example
static uint8_t popcount_tbl[65536] =
{
/* population count of all the integers 0 through 65535 */
};
int popcount (uint16_t num)
{
return popcount_tbl[num];
}
Where larger integers can be constructed by breaking them apart, for example with a 32-bit integer one can use popcount() on both the upper and lower 16-bits.
static int popcount32(uint32_t num)
{
return popcount(num & 0xFFFF) + popcount(num >> 16);
}
A more advanced algorithm that is also quicker, combining subtraction and bitwise AND:
int popcount(unsigned x)
{
int c = 0;
for (; x != 0; x &= x - 1)
c++;
return c;
}
Software support
Many programming languages provide a mechanism to perform population count either by implementing it in the language itself or by using intrinsic functions. Below is a short summary of some of them:
| Language | Compiler | Function |
|---|---|---|
| C | Visual Studio | __popcnt16() __popcnt() __popcnt64() |
| GCC | __builtin_popcount() __builtin_popcountl() __builtin_popcountll() | |
| C++ | - | std::bitset::count() |
| .NET Core (3.0+) | - | System.Numerics.BitOperations.PopCount() |
| Java | - | java.lang.Integer.bitCount() java.lang.Long.bitCount() java.math.BigInteger.bitCount() java.util.BitSet.cardinality() |
| MySQL | - | BIT_COUNT() |
| PHP | - | gmp_popcount() |
Hardware support
Various microprocessors have built-in support for count set bits.
| ISA | Extension | Mnemonic |
|---|---|---|
| X86 | SSE4 | POPCNT |
| ARM | NEON | VCNT |
| System/Z | - | POPCNT |