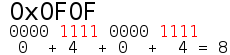From WikiChip
Difference between revisions of "population count"

(initial page)
(Added AVX-512 ISA.)
 
(10 intermediate revisions by 9 users not shown)
Line 1: Line 1:
−
[[File:Popcount.svg|right]]
+
{{title|Population Count (popcount)}}[[File:Popcount.svg|right]]
 
The '''population count''' (or '''popcount''') of a specific value is the number of [[set bits]] in that value. For example, the population count of {{hex|0F0F}}, {{hex|1111}}, and {{hex|00}} are {{dec|8}}, {{dec|4}}, and {{dec|0}} respectively.
 
The '''population count''' (or '''popcount''') of a specific value is the number of [[set bits]] in that value. For example, the population count of {{hex|0F0F}}, {{hex|1111}}, and {{hex|00}} are {{dec|8}}, {{dec|4}}, and {{dec|0}} respectively.
  
Line 10: Line 10:
 
int popcount(unsigned x)
 
int popcount(unsigned x)
 
{
 
{
−
     int c;
+
     int c = 0;
−
     for (c = 0; x != 0; x >>= 1)
+
     for (; x != 0; x >>= 1)
 
         if (x & 1)
 
         if (x & 1)
 
             c++;
 
             c++;
Line 37: Line 37:
 
{
 
{
 
     return popcount(num & 0xFFFF) + popcount(num >> 16);
 
     return popcount(num & 0xFFFF) + popcount(num >> 16);
 +
}
 +
</source>
 +
 +
A more advanced algorithm that is also quicker, combining subtraction and bitwise AND:
 +
 +
<source lang="c">
 +
int popcount(unsigned x)
 +
{
 +
    int c = 0;
 +
    for (; x != 0; x &= x - 1)
 +
        c++;
 +
    return c;
 
}
 
}
 
</source>
 
</source>
Line 50: Line 62:
 
|-
 
|-
 
| [[GCC]] || __builtin_popcount()<br />__builtin_popcountl()<br />__builtin_popcountll()
 
| [[GCC]] || __builtin_popcount()<br />__builtin_popcountl()<br />__builtin_popcountll()
 +
|-
 +
| [[C++]] || - || std::bitset::count()<br>std::popcount() since C++20
 +
|-
 +
| [[.NET Core (3.0+)]] || - || System.Numerics.BitOperations.PopCount()
 
|-
 
|-
 
| [[Java]] || - || java.lang.Integer.bitCount()<br />java.lang.Long.bitCount()<br />java.math.BigInteger.bitCount()<br />java.util.BitSet.cardinality()
 
| [[Java]] || - || java.lang.Integer.bitCount()<br />java.lang.Long.bitCount()<br />java.math.BigInteger.bitCount()<br />java.util.BitSet.cardinality()
−
|-
 
−
| [[C++]] || - || std::bitset::count()
 
 
|-
 
|-
 
| [[MySQL]] || - || BIT_COUNT()
 
| [[MySQL]] || - || BIT_COUNT()
 
|-
 
|-
 
| [[PHP]] || - || gmp_popcount()
 
| [[PHP]] || - || gmp_popcount()
 +
|-
 +
| [[python|Python (3.10+)]] || - || int.bit_count()
 +
|-
 +
| [[Rust]] || - || count_ones()
 
|}
 
|}
  
Line 65: Line 83:
 
{| class="wikitable sortable"
 
{| class="wikitable sortable"
 
|-
 
|-
−
! [[ISA]] !! Extension !! [[Mnemonic]]
+
! [[ISA]] !! Extension !! [[Mnemonic]] !!
 +
|-
 +
| rowspan="3" | [[X86]] || POPCNT || POPCNT || 16/32/64-bit operands
 +
|-
 +
| {{x86|AVX512_BITALG}} || VPOPCNTB/VPOPCNTW || Parallel population count on 8/16-bit operands in 128/256/512-bit vector
 
|-
 
|-
−
| [[X86]] || [[SSE4]] || POPCNT
+
| {{x86|AVX512_VPOPCNTDQ}} || VPOPCNTD/VPOPCNTQ || Parallel population count on 32/64-bit operands in 128/256/512-bit vector
 
|-
 
|-
−
| [[ARM]] || [[NEON]] || VCNT
+
| [[ARM]] || [[NEON]] || VCNT ||
 
|-
 
|-
−
| [[System/Z]] || - || POPCNT
+
| [[System/Z]] || - || POPCNT ||
 
|}
 
|}
 +
 +
==External links ==
 +
* [http://graphics.stanford.edu/~seander/bithacks.html#CountBitsSetParallel Counting bits set, in parallel]
  
 
[[Category:Binary arithmetic]]
 
[[Category:Binary arithmetic]]

Latest revision as of 00:55, 14 March 2023

Popcount.svg

The population count (or popcount) of a specific value is the number of set bits in that value. For example, the population count of 0F0F16, 111116, and 0016 are 810, 410, and 010 respectively.

Calculating the population count efficiently has been widely studied with implementations existing for both software and hardware. Many of the popular microprocessors also provide hardware support for this operation.

Implementations[edit]

The most basic implementation of a population count function as described in K&R can be written as 

int popcount(unsigned x)
{
    int c = 0;
    for (; x != 0; x >>= 1)
        if (x & 1)
            c++;
    return c;
}

If a large amount of memory is allowed to be used, one can precompile a large lookup table of population count and simply lookup the value from there every time. For example 

static uint8_t popcount_tbl[65536] =
{
  /* population count of all the integers 0 through 65535 */
};
int popcount (uint16_t num)
{
    return popcount_tbl[num];
}

Where larger integers can be constructed by breaking them apart, for example with a 32-bit integer one can use popcount() on both the upper and lower 16-bits. 

static int popcount32(uint32_t num)
{
    return popcount(num & 0xFFFF) + popcount(num >> 16);
}

A more advanced algorithm that is also quicker, combining subtraction and bitwise AND: 

int popcount(unsigned x)
{
    int c = 0;
    for (; x != 0; x &= x - 1)
        c++;
    return c;
}

Software support[edit]

Many programming languages provide a mechanism to perform population count either by implementing it in the language itself or by using intrinsic functions. Below is a short summary of some of them:

Language Compiler Function
C Visual Studio __popcnt16()
__popcnt()
__popcnt64()
GCC __builtin_popcount()
__builtin_popcountl()
__builtin_popcountll()
C++ - std::bitset::count()
std::popcount() since C++20
.NET Core (3.0+) - System.Numerics.BitOperations.PopCount()
Java - java.lang.Integer.bitCount()
java.lang.Long.bitCount()
java.math.BigInteger.bitCount()
java.util.BitSet.cardinality()
MySQL - BIT_COUNT()
PHP - gmp_popcount()
Python (3.10+) - int.bit_count()
Rust - count_ones()

Hardware support[edit]

Various microprocessors have built-in support for count set bits.

ISA Extension Mnemonic
X86 POPCNT POPCNT 16/32/64-bit operands
AVX512_BITALG VPOPCNTB/VPOPCNTW Parallel population count on 8/16-bit operands in 128/256/512-bit vector
AVX512_VPOPCNTDQ VPOPCNTD/VPOPCNTQ Parallel population count on 32/64-bit operands in 128/256/512-bit vector
ARM NEON VCNT
System/Z - POPCNT

External links[edit]

Retrieved from "https://en.wikichip.org/w/index.php?title=population_count&oldid=101205"