m |
|||
| (8 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | ''' | + | [[File:number systems.svg|right|300px]] |
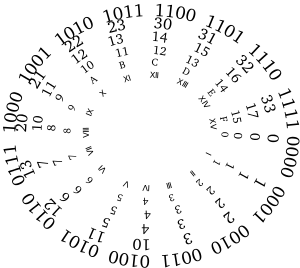
| + | A '''number system''' is a mathematical notation for representing numbers of a given [[number set|set]]. They are the foundation for conveying, quantifying, and manipulating [[data]]. | ||
| − | Number systems are mainly classified according to [[number notation|notations]] ([[positional notation]] vs [[sign-value notation]]) and their [[base]]. Today, we largely use the [[Arabic numerals]] which is a [[base-10]] positional notation numbering system. Machines on the other hand may use a different number system - such as the [[ | + | Number systems are mainly classified according to [[number notation|notations]] ([[positional notation]] vs [[sign-value notation]]) and their [[base]]. Today, we largely use the [[Arabic numerals]] which is a [[base-10]] positional notation numbering system. Machines on the other hand may use a different number system - such as the [[binary number system]]. |
== Notation == | == Notation == | ||
| Line 8: | Line 9: | ||
::<math>N_r = (d_{n-2} d_{n-1} \cdots d_2 d_1 d_0 \cdot d_{-1} d_{-2} d_{-3} \cdots d_{-m})_r</math> | ::<math>N_r = (d_{n-2} d_{n-1} \cdots d_2 d_1 d_0 \cdot d_{-1} d_{-2} d_{-3} \cdots d_{-m})_r</math> | ||
| − | Where '''r''' is the [[radix]] or the number of digits in the number system | + | Where '''r''' is the [[radix]] or base. The base represents the number of digits in the number system. '''d''' are the digits defined for that given radix. The dot in the center ('''⋅''') is known as the [[radix point]]. It separates the integer part on the left from the fractional portion on the right. Furthermore, the value of number ''N'' in base ''r'' can be represented in '''polynomial form''' as |
::<math>N_r = \sum^{n-1}_{i=-m} d_i r^i= (d_{n-2}r^{n-2} + d_{n-1}r^{n-1} + \cdots + d_1r^1 + d_0r^0 + d_{-1}r^{-1} + d_{-2}r^{-2} + d_{-m}r^{-m})_r</math> | ::<math>N_r = \sum^{n-1}_{i=-m} d_i r^i= (d_{n-2}r^{n-2} + d_{n-1}r^{n-1} + \cdots + d_1r^1 + d_0r^0 + d_{-1}r^{-1} + d_{-2}r^{-2} + d_{-m}r^{-m})_r</math> | ||
| − | Where '''d''' is the digit in the ith position. | + | Where '''d''' is the digit in the ith position. When a number has no fractional portion, the number can be more accurately called an [[integer]]. Conversely, if a number has no integer part, it is called a fractional number or simply a [[fraction]]. |
| − | + | On various occasions, a number might be written in the form <math>N_r</math> where the subscript ''r'' is the [[radix]] of number ''N''. Subscripts are used to indicate a [[base]]; often, to avoid confusion, when presenting values in different basis. | |
| − | + | ||
| + | === Decimal Number System === | ||
| + | {{main|decimal}} | ||
| + | For the most part, humans use the decimal number system (base-10) for all day-to-day activities. It is the number system we learn and grow up with hence the most familiar to us. In a base-10 number system there are 10 distinct digits: <math>\{0,1,2,3,4,5,6,7,8,9\}</math>. Consider the following number <math>49835.5825_{10}</math>. Note the ''10''. We can express that number in polynomial form as | ||
::<math> | ::<math> | ||
| − | \begin{ | + | \begin{align} |
| − | N_{10} &= | + | N_{10} &= 49835.5825 \\ |
| − | &= | + | &= (d_4 d_3 d_2 d_1 d_0 \cdot d_{-1} d_{-2} d_{-3} d_{-4})_{10} \\ |
| − | &= | + | &= 4 \times 10^4 + 9 \times 10^3 + 8 \times 10^2 + 3 \times 10^1 + 5 \times 10^0 + 5 \times 10^{-1} + 8 \times 10^{-2} + 2 \times 10^{-3} + 5 \times 10^{-4} \\ |
| − | &= | + | &= 40000 + 9000 + 800 + 30 + 5 + 0.5 + 0.08 + 0.002 + 0.0005 \\ |
| − | &= | + | &= 49835.5825_{10} |
| − | \end{ | + | \end{align} |
</math> | </math> | ||
| + | Now consider the fractional decimal number <math>0.938_{10}</math>. Since there is no integer part, our exponents start at 0 and decrease with each additional digit: | ||
| + | |||
| + | ::<math> | ||
| + | \begin{align} | ||
| + | N_{10} &= 0.938 \\ | ||
| + | &= (d_{-1} d_{-2} d_{-3})_{10} \\ | ||
| + | &= 9 \times 10^{-1} + 3 \times 10^{-2} + 8 \times 10^{-3} \\ | ||
| + | &= 0.9 + 0.03 + 0.008 \\ | ||
| + | &= 0.938_{10} | ||
| + | \end{align} | ||
| + | </math> | ||
| − | + | === Binary Number System === | |
| + | {{main|binary}} | ||
| + | In the binary number system, the [[radix]] is 2 - i.e. a number system capable of only representing two discrete values: <math>\{0,1\}</math>. Let's consider the following number <math>10101110.011_{2}</math>. Note that the subscript is ''2''. We can express this [[binary number]] in polynomial form as follows: | ||
::<math> | ::<math> | ||
| − | \begin{ | + | \begin{align} |
| − | N_{2} &= | + | N_{2} &= 10101110.011 \\ |
| − | &= | + | &= (d_7 d_6 d_5 d_4 d_3 d_2 d_1 d_0 \cdot d_{-1} d_{-2} d_{-3})_{2} \\ |
| − | &= | + | &= 1 \times 2^7 + 0 \times 2^6 + 1 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 + 0 \times 2^{-1} + 1 \times 2^{-2} + 1 \times 2^{-3} \\ |
| − | &= | + | &= 128 + 32 + 8 + 4 + 2 + 0.25 + 0.125 \\ |
| − | &= | + | &= 174.375_{10} \\ |
| − | \end{ | + | \end{align} |
</math> | </math> | ||
| − | Note that as part of the process we've actually converted the number to decimal. | + | Note that as part of the process we've actually converted the number to [[decimal]]. |
| − | + | === Octal Number System === | |
| − | + | {{main|octal}} | |
| + | The octal number system as the name implies uses [[radix]] of 8; i.e. the number system is represented via 8 discrete values: <math>\{0,1,2,3,4,5,6,7\}</math>. Let's take the number <math>703.104_8</math>, | ||
::<math> | ::<math> | ||
| − | \begin{ | + | \begin{align} |
| − | N_{ | + | N_{8} &= 703.104 \\ |
| − | &= | + | &= (d_2 d_1 d_0 \cdot d_{-1} d_{-2} d_{-3})_{16} \\ |
| − | &= | + | &= 7 \times 8^2 + 0 \times 8^1 + 3 \times 8^0 + 1 \times 8^{-1} + 0 \times 8^{-2} + 4 \times 8^{-3} \\ |
| − | + | &= 448 + 3 + 0.125 + 0.0078125 \\ | |
| − | &= | + | &= 451.1328125_{10} |
| − | & | + | \end{align} |
| − | \end{ | ||
</math> | </math> | ||
| − | |||
| + | An interesting property of a base-8 system being <math>2^3</math> is that converting a number from [[binary]] to [[octal]] can easily done by breaking the number number into groups of 3 [[bit]]s and converting each group individually into octal. Octal being 8 values means each group of 3 binary bits equates to a single octal digit. For example consider the following number <math>1010011101_2</math>. We can break the number into groups of 3 bits: <math>[001]_2 [010]_2 [011]_2 [101]_2</math>. Each of those groups can now be converted to octal independently: <math>[1]_8 [2]_8 [3]_8 [5]_8 = 1235_8</math>. Note that the conversion from octal back to binary can just as easily be done by simple converting each individual octal digit back into a group of 3 binary digits. | ||
| − | + | === Hexadecimal Number System === | |
| + | {{main|Hexadecimal}} | ||
| + | The Hexadecimal number system or base-16 has 16 discrete digits. Those digits have traditionally been <math>\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F\}</math>. Note that A through F are decimal 10 through 15, respectively. In this example we'll use the [[hexadecimal|hex]] number <math>FDAE.F5F_{16}</math>. | ||
::<math> | ::<math> | ||
| − | \begin{ | + | \begin{align} |
| − | N_{ | + | N_{16} &= FDAE.F5F \\ |
| − | &= | + | &= (d_3 d_2 d_1 d_0 \cdot d_{-1} d_{-2})_{16} \\ |
| − | &= | + | &= F \times 16^3 + D \times 16^2 + A \times 16^1 + E \times 16^0 + F \times 16^{-1} + 5 \times 16^{-2} + F \times 16^{-3} \\ |
| − | &= | + | &= 15 \times 16^3 + 13 \times 16^2 + 10 \times 16^1 + 14 \times 16^0 + 15 \times 16^{-1} + 5 \times 16^{-2} + 15 \times 16^{-3} \\ |
| − | & | + | &= 61440 + 3328 + 160 + 15 + 0.9375 + 0.01953125 + 0.003662109375 \\ |
| − | \end{ | + | &\cong 64943.9606934_{10} |
| + | \end{align} | ||
</math> | </math> | ||
| + | |||
| + | Note that the final value is rounded as a result of fraction estimation. Note that just like [[octal]] is also a power of 2 (<math>2^4</math>), meaning conversion from binary to hex can be done by simply breaking down a [[binary number]] into groups of 4 bits and converting each group individually. For example, consider the number <math>101101011110001_2</math> which can be broken down into <math>[0101]_2[1010]_2[1111]_2[0001]_2 = [5]_{16}[A]_{16}[F]_{16}[1]_{16} = 5AF1_{16}</math>. Converting a number back from hex to binary is done by simply converting each individual hex digit back into a group of 4 bits. | ||
Latest revision as of 06:08, 2 December 2015
A number system is a mathematical notation for representing numbers of a given set. They are the foundation for conveying, quantifying, and manipulating data.
Number systems are mainly classified according to notations (positional notation vs sign-value notation) and their base. Today, we largely use the Arabic numerals which is a base-10 positional notation numbering system. Machines on the other hand may use a different number system - such as the binary number system.
Contents
Notation[edit]
In the positional notation, numbers are a string consisting of one or more juxtaposed digits. For example, fixed-point form number N takes the following form:
Where r is the radix or base. The base represents the number of digits in the number system. d are the digits defined for that given radix. The dot in the center (⋅) is known as the radix point. It separates the integer part on the left from the fractional portion on the right. Furthermore, the value of number N in base r can be represented in polynomial form as
Where d is the digit in the ith position. When a number has no fractional portion, the number can be more accurately called an integer. Conversely, if a number has no integer part, it is called a fractional number or simply a fraction.
On various occasions, a number might be written in the form where the subscript r is the radix of number N. Subscripts are used to indicate a base; often, to avoid confusion, when presenting values in different basis.
Decimal Number System[edit]
- Main article: decimal
For the most part, humans use the decimal number system (base-10) for all day-to-day activities. It is the number system we learn and grow up with hence the most familiar to us. In a base-10 number system there are 10 distinct digits: . Consider the following number . Note the 10. We can express that number in polynomial form as
Now consider the fractional decimal number . Since there is no integer part, our exponents start at 0 and decrease with each additional digit:
Binary Number System[edit]
- Main article: binary
In the binary number system, the radix is 2 - i.e. a number system capable of only representing two discrete values: . Let's consider the following number . Note that the subscript is 2. We can express this binary number in polynomial form as follows:
Note that as part of the process we've actually converted the number to decimal.
Octal Number System[edit]
- Main article: octal
The octal number system as the name implies uses radix of 8; i.e. the number system is represented via 8 discrete values: . Let's take the number ,
An interesting property of a base-8 system being is that converting a number from binary to octal can easily done by breaking the number number into groups of 3 bits and converting each group individually into octal. Octal being 8 values means each group of 3 binary bits equates to a single octal digit. For example consider the following number . We can break the number into groups of 3 bits: . Each of those groups can now be converted to octal independently: . Note that the conversion from octal back to binary can just as easily be done by simple converting each individual octal digit back into a group of 3 binary digits.
Hexadecimal Number System[edit]
- Main article: Hexadecimal
The Hexadecimal number system or base-16 has 16 discrete digits. Those digits have traditionally been . Note that A through F are decimal 10 through 15, respectively. In this example we'll use the hex number .
Note that the final value is rounded as a result of fraction estimation. Note that just like octal is also a power of 2 (), meaning conversion from binary to hex can be done by simply breaking down a binary number into groups of 4 bits and converting each group individually. For example, consider the number which can be broken down into . Converting a number back from hex to binary is done by simply converting each individual hex digit back into a group of 4 bits.