Amdahl's Law is a formulation an observation that attempts to give an upper bound on the performance increase that can be realized when a fixed workload is moved to a more parallel environment (e.g. multiprocessing or multi-core environment). The law is named after Dr. Gene M. Amdahl who first addressed the problem in his 1967 paper "Validity of the single processor approach to achieving large scale computing capabilities".
Amdahl's Law says that for fixed workloads, the upper bound of the speedup expected from moving to a more parallelized environment gets dominated by the sequential portion of the code as the parallel portion gets further divided into smaller and smaller chunks.
Theory
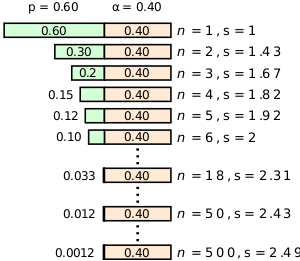
Consider a program executing on a single-core uniprocessor computer. Suppose this program is operating on a fixed workload with a total execution time of minutes. Now let's suppose we want to divide or partition this program to execute over multiple nodes (e.g., cores). Some fraction, , of the program's code cannot be parallelized and must be executed sequentially. This portion of the program is the sequential bottleneck.
The portion of the program that can be executed in parallel is therefore . Since no speedup is obtained from the sequential bottleneck portion of the program, regardless of the number of execution nodes, it always accounts for of the time. Likewise, the execution time of the parallel portion of the program decreases linearly with more node, i.e., speedup is obtained.
Amdahl's Law states that the speedup factor for spanning a program across nodes over the use of a single processing node can be expressed as:
It can be seen that the greatest speedup is only obtained if the sequential bottleneck portion of the program is eliminated (i.e., ). In such situations as the number of nodes becomes sufficiently large (i.e., ), the speedup approaches . It can be seen that the upper bound on the speedup is actually independent of the number of nodes but instead is entirely limited by the sequential bottleneck part of the program which cannot be parallelized.
Example
Suppose you want to achieve a speedup of 80 with just 100 cores. That is, . This requires or 99.7475% of the program's execution to be parallelizable.